Controlled Causal Hallucinations Can Estimate Phantom Nodes in Multiexpert Mixtures of Fuzzy Cognitive Maps

An adaptive multiexpert mixture of feedback causal models can approximate missing or phantom nodes in large-scale causal models. The result gives a scalable form of \emph{big knowledge}. The mixed model approximates a sampled dynamical system by approximating its main limit-cycle equilibria. Each expert first draws a fuzzy cognitive map (FCM) with at least one missing causal node or variable. FCMs are directed signed partial-causality cyclic graphs. They mix naturally through convex combination to produce a new causal feedback FCM. Supervised learning helps each expert FCM estimate its phantom node by comparing the FCM's partial equilibrium with the complete multi-node equilibrium. Such phantom-node estimation allows partial control over these causal hallucinations and helps approximate the future trajectory of the dynamical system. But the approximation can be computationally heavy. Mixing the tuned expert FCMs gives a practical way to find several phantom nodes and thereby better approximate the feedback system's true equilibrium behavior.

Training Deep Neural Classifiers with Soft Diamond Regularizers

We introduce new \emph{soft diamond} regularizers that both improve synaptic sparsity and maintain classification accuracy in deep neural networks. These parametrized regularizers outperform the state-of-the-art hard-diamond Laplacian regularizer of Lasso regression and classification. They use thick-tailed symmetric alpha-stable ($\mathcal{S \alpha S}$) bell-curve synaptic weight priors that are not Gaussian and so have thicker tails. The geometry of the diamond-shaped constraint set varies from a circle to a star depending on the tail thickness and dispersion of the prior probability density function. Training directly with these priors is computationally intensive because almost all $\mathcal{S \alpha S}$ probability densities lack a closed form. A precomputed look-up table removed this computational bottleneck. We tested the new soft diamond regularizers with deep neural classifiers on the three datasets CIFAR-10, CIFAR-100, and Caltech-256. The regularizers improved the accuracy of the classifiers. The improvements included $4.57\%$ on CIFAR-10, $4.27\%$ on CIFAR-100, and $6.69\%$ on Caltech-256. They also outperformed $L_2$ regularizers on all the test cases. Soft diamond regularizers also outperformed $L_1$ lasso or Laplace regularizers because they better increased sparsity while improving classification accuracy. Soft-diamond priors substantially improved accuracy on CIFAR-10 when combined with dropout, batch, or data-augmentation regularization.

Beyond DAGs: Modeling Causal Feedback with Fuzzy Cognitive Maps

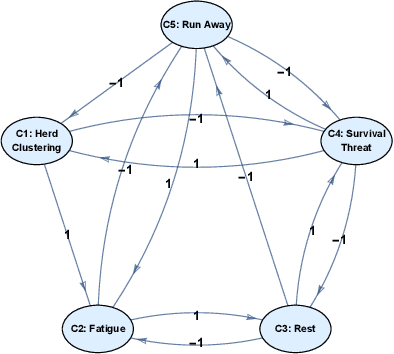
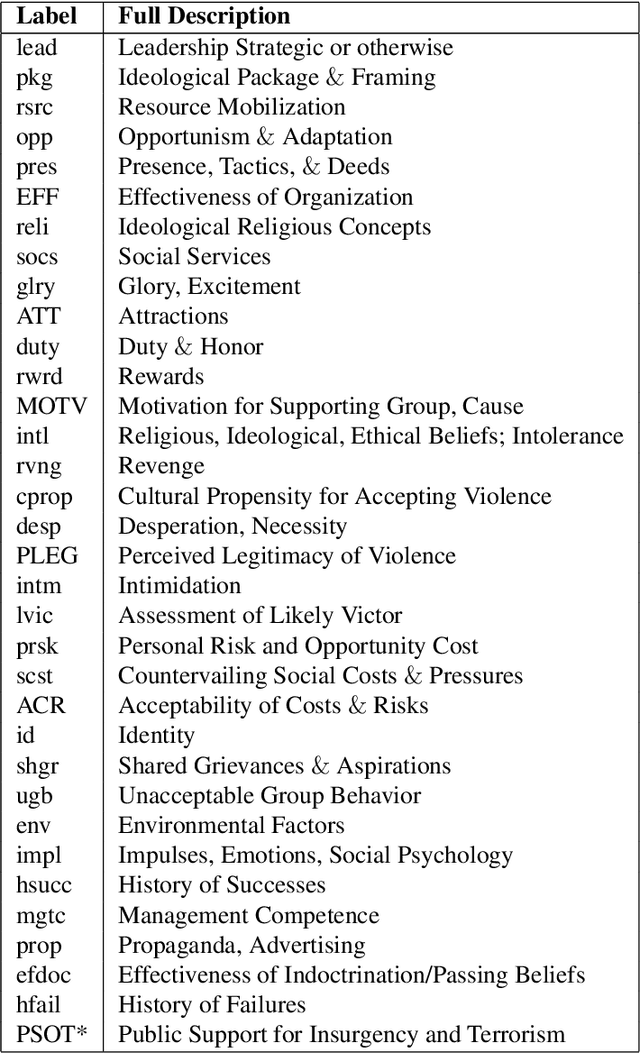
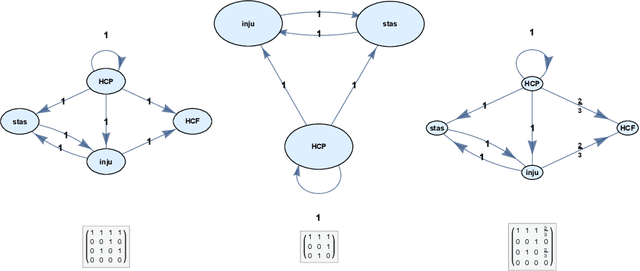
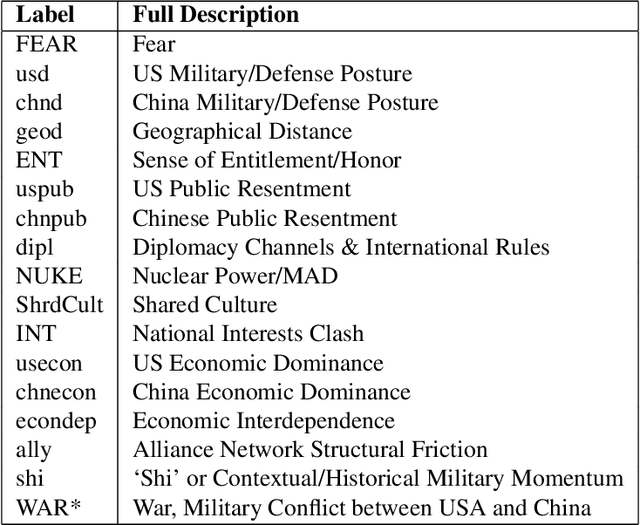
Fuzzy cognitive maps (FCMs) model feedback causal relations in interwoven webs of causality and policy variables. FCMs are fuzzy signed directed graphs that allow degrees of causal influence and event occurrence. Such causal models can simulate a wide range of policy scenarios and decision processes. Their directed loops or cycles directly model causal feedback. Their nonlinear dynamics permit forward-chaining inference from input causes and policy options to output effects. Users can add detailed dynamics and feedback links directly to the causal model or infer them with statistical learning laws. Users can fuse or combine FCMs from multiple experts by weighting and adding the underlying fuzzy edge matrices and do so recursively if needed. The combined FCM tends to better represent domain knowledge as the expert sample size increases if the expert sample approximates a random sample. Many causal models use more restrictive directed acyclic graphs (DAGs) and Bayesian probabilities. DAGs do not model causal feedback because they do not contain closed loops. Combining DAGs also tends to produce cycles and thus tends not to produce a new DAG. Combining DAGs tends to produce a FCM. FCM causal influence is also transitive whereas probabilistic causal influence is not transitive in general. Overall: FCMs trade the numerical precision of probabilistic DAGs for pattern prediction, faster and scalable computation, ease of combination, and richer feedback representation. We show how FCMs can apply to problems of public support for insurgency and terrorism and to US-China conflict relations in Graham Allison's Thucydides-trap framework. The appendix gives the textual justification of the Thucydides-trap FCM. It also extends our earlier theorem [Osoba-Kosko2017] to a more general result that shows the transitive and total causal influence that upstream concept nodes exert on downstream nodes.

Noisy Expectation-Maximization: Applications and Generalizations

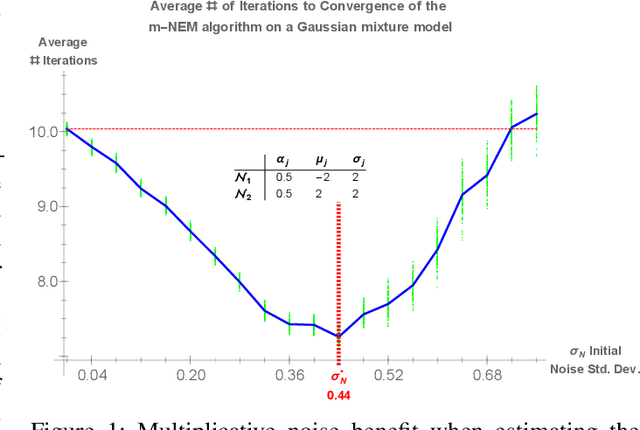
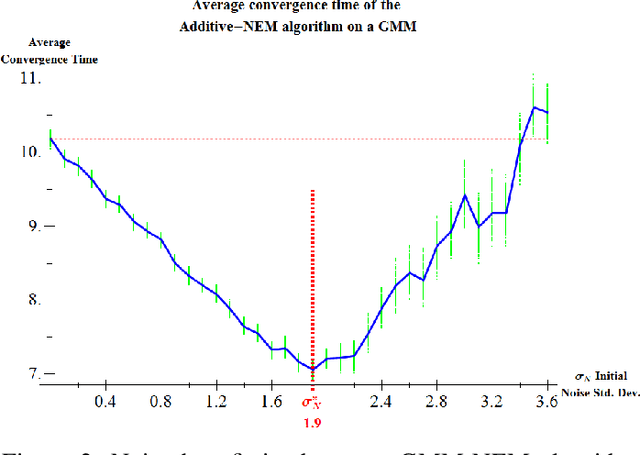
We present a noise-injected version of the Expectation-Maximization (EM) algorithm: the Noisy Expectation Maximization (NEM) algorithm. The NEM algorithm uses noise to speed up the convergence of the EM algorithm. The NEM theorem shows that injected noise speeds up the average convergence of the EM algorithm to a local maximum of the likelihood surface if a positivity condition holds. The generalized form of the noisy expectation-maximization (NEM) algorithm allow for arbitrary modes of noise injection including adding and multiplying noise to the data. We demonstrate these noise benefits on EM algorithms for the Gaussian mixture model (GMM) with both additive and multiplicative NEM noise injection. A separate theorem (not presented here) shows that the noise benefit for independent identically distributed additive noise decreases with sample size in mixture models. This theorem implies that the noise benefit is most pronounced if the data is sparse. Injecting blind noise only slowed convergence.