Privacy-Preserving Race/Ethnicity Estimation for Algorithmic Bias Measurement in the U.S

AI fairness measurements, including tests for equal treatment, often take the form of disaggregated evaluations of AI systems. Such measurements are an important part of Responsible AI operations. These measurements compare system performance across demographic groups or sub-populations and typically require member-level demographic signals such as gender, race, ethnicity, and location. However, sensitive member-level demographic attributes like race and ethnicity can be challenging to obtain and use due to platform choices, legal constraints, and cultural norms. In this paper, we focus on the task of enabling AI fairness measurements on race/ethnicity for \emph{U.S. LinkedIn members} in a privacy-preserving manner. We present the Privacy-Preserving Probabilistic Race/Ethnicity Estimation (PPRE) method for performing this task. PPRE combines the Bayesian Improved Surname Geocoding (BISG) model, a sparse LinkedIn survey sample of self-reported demographics, and privacy-enhancing technologies like secure two-party computation and differential privacy to enable meaningful fairness measurements while preserving member privacy. We provide details of the PPRE method and its privacy guarantees. We then illustrate sample measurement operations. We conclude with a review of open research and engineering challenges for expanding our privacy-preserving fairness measurement capabilities.

Policy Gradients for Optimal Parallel Tempering MCMC

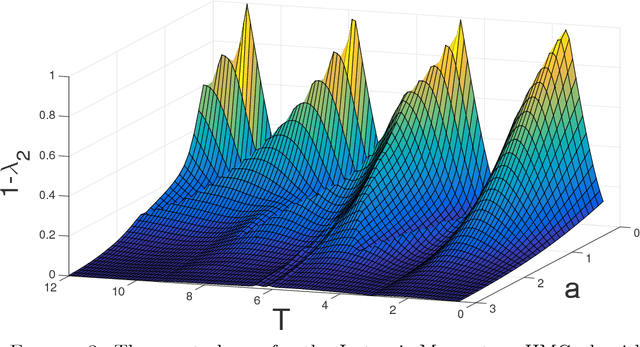
Parallel tempering is meta-algorithm for Markov Chain Monte Carlo that uses multiple chains to sample from tempered versions of the target distribution, enhancing mixing in multi-modal distributions that are challenging for traditional methods. The effectiveness of parallel tempering is heavily influenced by the selection of chain temperatures. Here, we present an adaptive temperature selection algorithm that dynamically adjusts temperatures during sampling using a policy gradient approach. Experiments demonstrate that our method can achieve lower integrated autocorrelation times compared to traditional geometrically spaced temperatures and uniform acceptance rate schemes on benchmark distributions.

Optimal Scaling for the Proximal Langevin Algorithm in High Dimensions

The Metropolis-adjusted Langevin (MALA) algorithm is a sampling algorithm that incorporates the gradient of the logarithm of the target density in its proposal distribution. In an earlier joint work \cite{pill:stu:12}, the author had extended the seminal work of \cite{Robe:Rose:98} and showed that in stationarity, MALA applied to an $N$-dimensional approximation of the target will take ${\cal O}(N^{\frac13})$ steps to explore its target measure. It was also shown in \cite{Robe:Rose:98,pill:stu:12} that, as a consequence of the diffusion limit, the MALA algorithm is optimized at an average acceptance probability of $0.574$. In \cite{pere:16}, Pereyra introduced the proximal MALA algorithm where the gradient of the log target density is replaced by the proximal function (mainly aimed at implementing MALA non-differentiable target densities). In this paper, we show that for a wide class of twice differentiable target densities, the proximal MALA enjoys the same optimal scaling as that of MALA in high dimensions and also has an average optimal acceptance probability of $0.574$. The results of this paper thus give the following practically useful guideline: for smooth target densities where it is expensive to compute the gradient while implementing MALA, users may replace the gradient with the corresponding proximal function (that can be often computed relatively cheaply via convex optimization) \emph{without} losing any efficiency. This confirms some of the empirical observations made in \cite{pere:16}.

Does Hamiltonian Monte Carlo mix faster than a random walk on multimodal densities?

Hamiltonian Monte Carlo (HMC) is a very popular and generic collection of Markov chain Monte Carlo (MCMC) algorithms. One explanation for the popularity of HMC algorithms is their excellent performance as the dimension $d$ of the target becomes large: under conditions that are satisfied for many common statistical models, optimally-tuned HMC algorithms have a running time that scales like $d^{0.25}$. In stark contrast, the running time of the usual Random-Walk Metropolis (RWM) algorithm, optimally tuned, scales like $d$. This superior scaling of the HMC algorithm with dimension is attributed to the fact that it, unlike RWM, incorporates the gradient information in the proposal distribution. In this paper, we investigate a different scaling question: does HMC beat RWM for highly $\textit{multimodal}$ targets? We find that the answer is often $\textit{no}$. We compute the spectral gaps for both the algorithms for a specific class of multimodal target densities, and show that they are identical. The key reason is that, within one mode, the gradient is effectively ignorant about other modes, thus negating the advantage the HMC algorithm enjoys in unimodal targets. We also give heuristic arguments suggesting that the above observation may hold quite generally. Our main tool for answering this question is a novel simple formula for the conductance of HMC using Liouville's theorem. This result allows us to compute the spectral gap of HMC algorithms, for both the classical HMC with isotropic momentum and the recent Riemannian HMC, for multimodal targets.