Fully Adaptive Composition in Differential Privacy

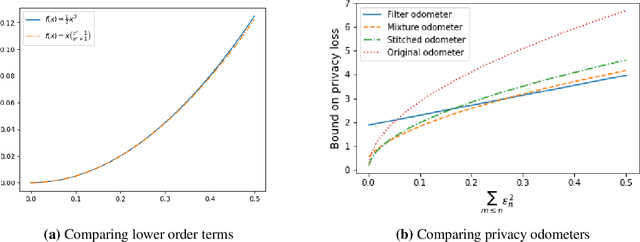
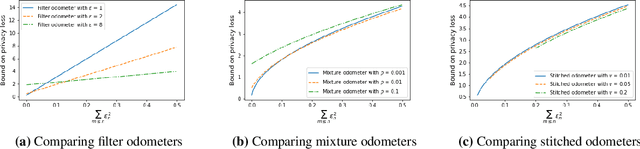
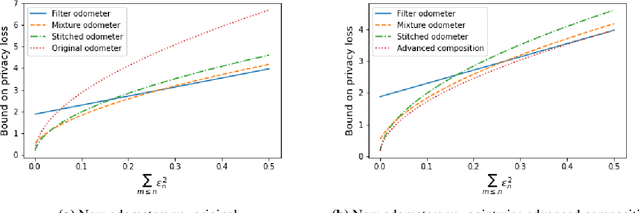
Composition is a key feature of differential privacy. Well-known advanced composition theorems allow one to query a private database quadratically more times than basic privacy composition would permit. However, these results require that the privacy parameters of all algorithms be fixed before interacting with the data. To address this, Rogers et al. introduced fully adaptive composition, wherein both algorithms and their privacy parameters can be selected adaptively. The authors introduce two probabilistic objects to measure privacy in adaptive composition: privacy filters, which provide differential privacy guarantees for composed interactions, and privacy odometers, time-uniform bounds on privacy loss. There are substantial gaps between advanced composition and existing filters and odometers. First, existing filters place stronger assumptions on the algorithms being composed. Second, these odometers and filters suffer from large constants, making them impractical. We construct filters that match the tightness of advanced composition, including constants, despite allowing for adaptively chosen privacy parameters. We also construct several general families of odometers. These odometers can match the tightness of advanced composition at an arbitrary, preselected point in time, or at all points in time simultaneously, up to a doubly-logarithmic factor. We obtain our results by leveraging recent advances in time-uniform martingale concentration. In sum, we show that fully adaptive privacy is obtainable at almost no loss, and conjecture that our results are essentially unimprovable (even in constants) in general.