Parameter Estimation Bounds Based on the Theory of Spectral Lines
Paper and Code
Jun 23, 2020

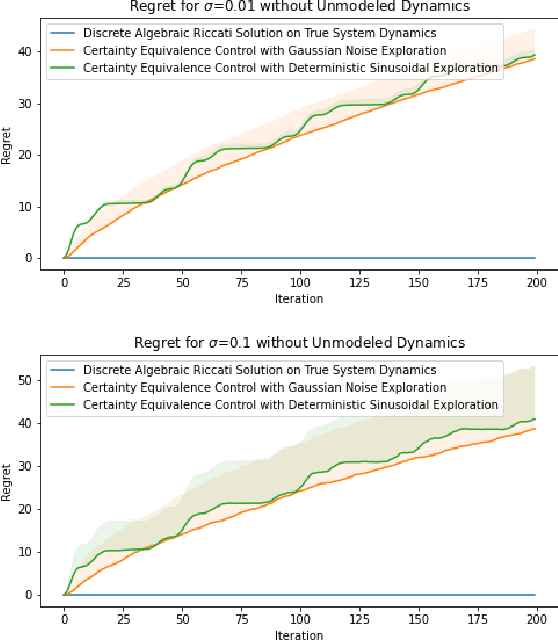
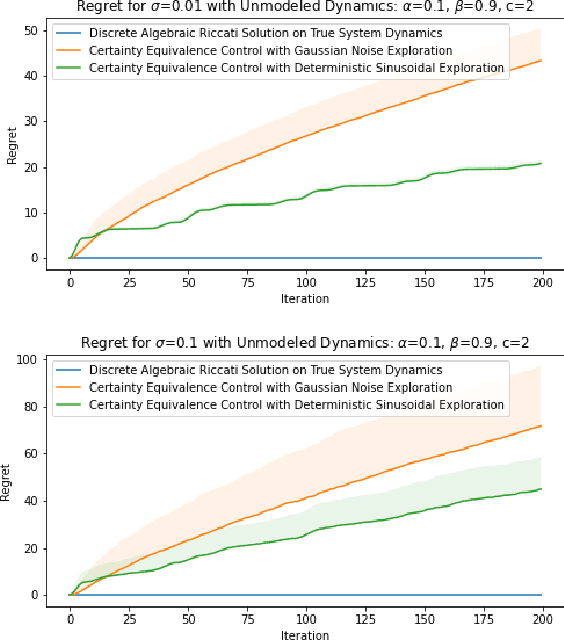
Recent methods in the machine learning literature have proposed a Gaussian noise-based exogenous signal to learn the parameters of a dynamic system. In this paper, we propose the use of a spectral lines-based deterministic exogenous signal to solve the same problem. Our theoretical analysis consists of a new toolkit which employs the theory of spectral lines, retains the stochastic setting, and leads to non-asymptotic bounds on the parameter estimation error. The results are shown to lead to a tunable parameter identification error. In particular, it is shown that the identification error can be minimized through an an optimal choice of the spectrum of the exogenous signal.
* Submitted to Neurips 2020
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge