Data-Driven Robust Optimization for Energy-Aware and Safe Navigation of Electric Vehicles

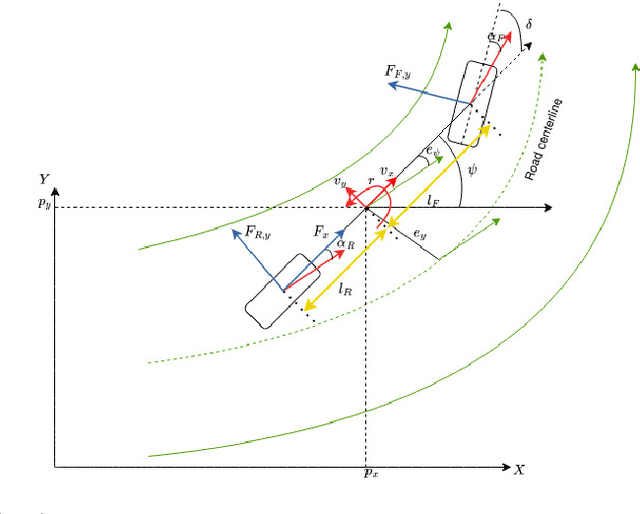
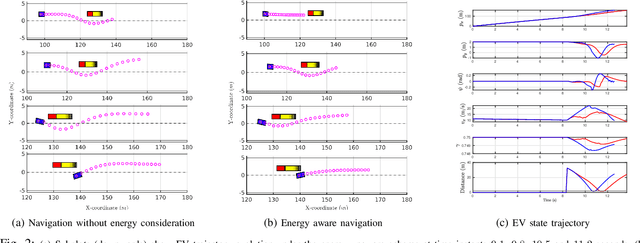
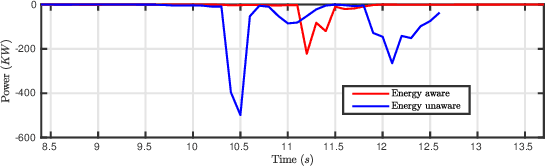
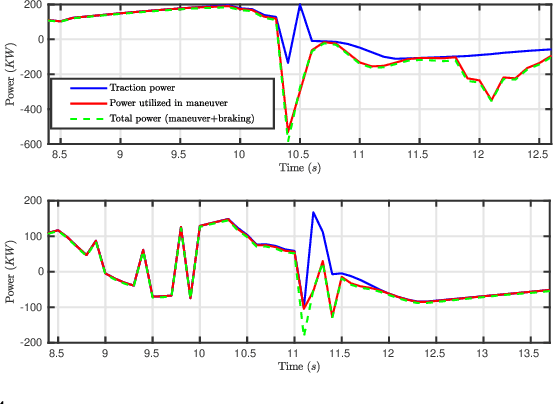
In this paper, we simultaneously tackle the problem of energy optimal and safe navigation of electric vehicles in a data-driven robust optimization framework. We consider a dynamic model of the electric vehicle which includes both longitudinal and lateral motion as well as dynamics of stored energy level. We leverage past data of obstacle motion to construct a future occupancy set with probabilistic guarantees, and formulate robust collision avoidance constraints with respect to such an occupancy set using convex programming duality. Consequently, we present the finite horizon optimal control problem subject to robust collision avoidance constraints while penalizing resulting energy consumption. Finally, we show the effectiveness of the proposed techniques in reducing energy consumption and ensuring safe navigation via extensive simulations.

Generalized Gradient Flows with Provable Fixed-Time Convergence and Fast Evasion of Non-Degenerate Saddle Points

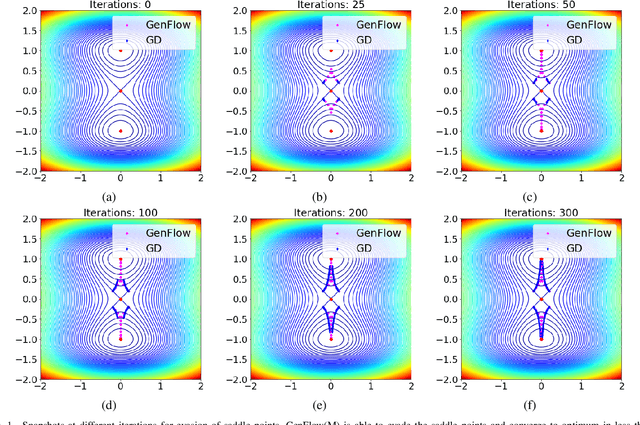
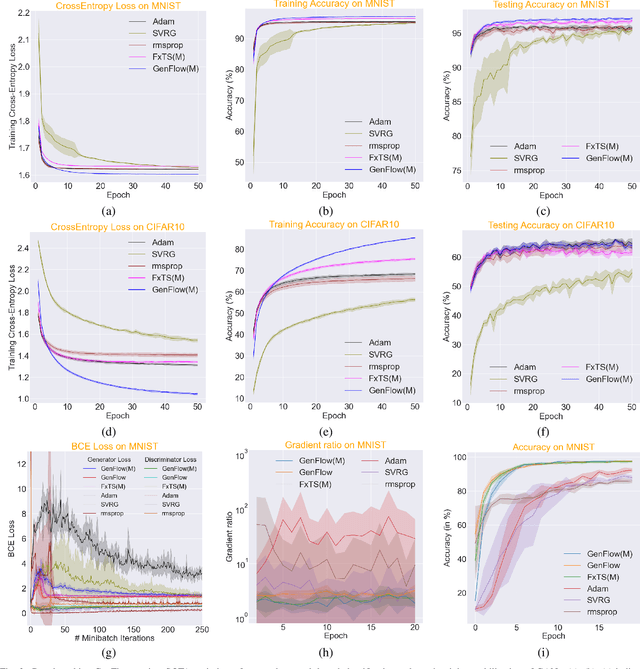
Gradient-based first-order convex optimization algorithms find widespread applicability in a variety of domains, including machine learning tasks. Motivated by the recent advances in fixed-time stability theory of continuous-time dynamical systems, we introduce a generalized framework for designing accelerated optimization algorithms with strongest convergence guarantees that further extend to a subclass of non-convex functions. In particular, we introduce the \emph{GenFlow} algorithm and its momentum variant that provably converge to the optimal solution of objective functions satisfying the Polyak-{\L}ojasiewicz (PL) inequality, in a fixed-time. Moreover for functions that admit non-degenerate saddle-points, we show that for the proposed GenFlow algorithm, the time required to evade these saddle-points is bounded uniformly for all initial conditions. Finally, for strongly convex-strongly concave minimax problems whose optimal solution is a saddle point, a similar scheme is shown to arrive at the optimal solution again in a fixed-time. The superior convergence properties of our algorithm are validated experimentally on a variety of benchmark datasets.

Data-Driven Risk-sensitive Model Predictive Control for Safe Navigation in Multi-Robot Systems

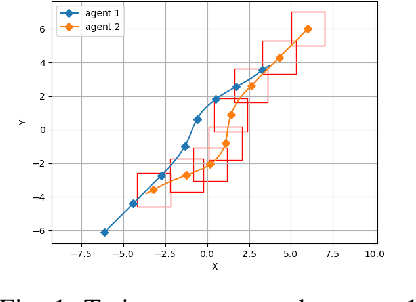
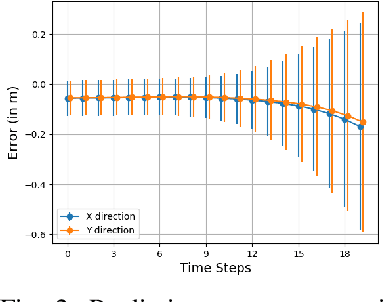
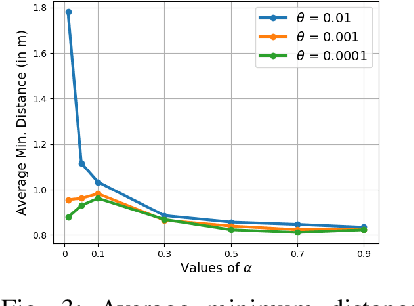
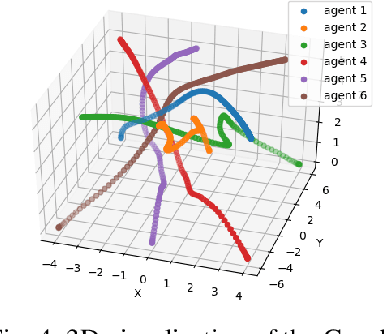
Safe navigation is a fundamental challenge in multi-robot systems due to the uncertainty surrounding the future trajectory of the robots that act as obstacles for each other. In this work, we propose a principled data-driven approach where each robot repeatedly solves a finite horizon optimization problem subject to collision avoidance constraints with latter being formulated as distributionally robust conditional value-at-risk (CVaR) of the distance between the agent and a polyhedral obstacle geometry. Specifically, the CVaR constraints are required to hold for all distributions that are close to the empirical distribution constructed from observed samples of prediction error collected during execution. The generality of the approach allows us to robustify against prediction errors that arise under commonly imposed assumptions in both distributed and decentralized settings. We derive tractable finite-dimensional approximations of this class of constraints by leveraging convex and minmax duality results for Wasserstein distributionally robust optimization problems. The effectiveness of the proposed approach is illustrated in a multi-drone navigation setting implemented in Gazebo platform.