MorphEUS: Morphable Omnidirectional Unmanned System

Omnidirectional aerial vehicles (OMAVs) have opened up a wide range of possibilities for inspection, navigation, and manipulation applications using drones. In this paper, we introduce MorphEUS, a morphable co-axial quadrotor that can control position and orientation independently with high efficiency. It uses a paired servo motor mechanism for each rotor arm, capable of pointing the vectored-thrust in any arbitrary direction. As compared to the \textit{state-of-the-art} OMAVs, we achieve higher and more uniform force/torque reachability with a smaller footprint and minimum thrust cancellations. The overactuated nature of the system also results in resiliency to rotor or servo-motor failures. The capabilities of this quadrotor are particularly well-suited for contact-based infrastructure inspection and close-proximity imaging of complex geometries. In the accompanying control pipeline, we present theoretical results for full controllability, almost-everywhere exponential stability, and thrust-energy optimality. We evaluate our design and controller on high-fidelity simulations showcasing the trajectory-tracking capabilities of the vehicle during various tasks. Supplementary details and experimental videos are available on the project webpage.

Data-Driven Risk-sensitive Model Predictive Control for Safe Navigation in Multi-Robot Systems

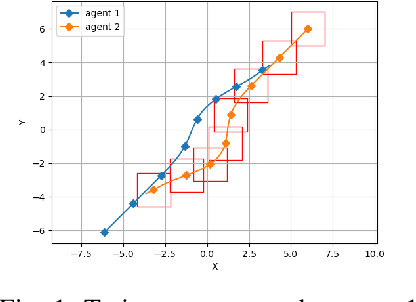
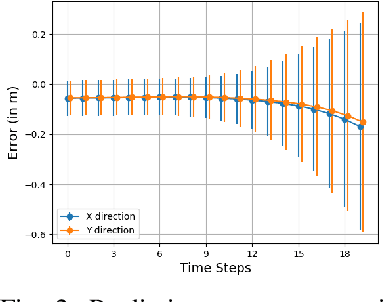
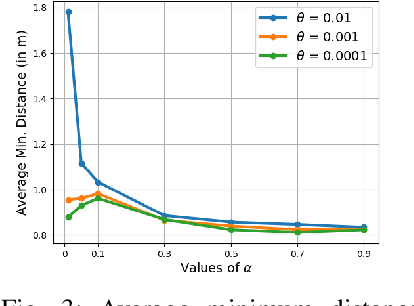
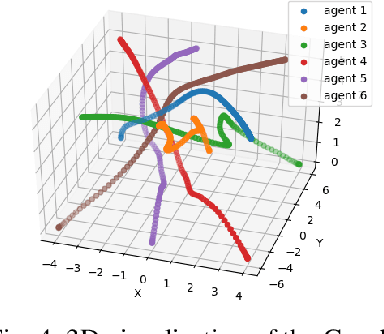
Safe navigation is a fundamental challenge in multi-robot systems due to the uncertainty surrounding the future trajectory of the robots that act as obstacles for each other. In this work, we propose a principled data-driven approach where each robot repeatedly solves a finite horizon optimization problem subject to collision avoidance constraints with latter being formulated as distributionally robust conditional value-at-risk (CVaR) of the distance between the agent and a polyhedral obstacle geometry. Specifically, the CVaR constraints are required to hold for all distributions that are close to the empirical distribution constructed from observed samples of prediction error collected during execution. The generality of the approach allows us to robustify against prediction errors that arise under commonly imposed assumptions in both distributed and decentralized settings. We derive tractable finite-dimensional approximations of this class of constraints by leveraging convex and minmax duality results for Wasserstein distributionally robust optimization problems. The effectiveness of the proposed approach is illustrated in a multi-drone navigation setting implemented in Gazebo platform.