Low Rank Multi-Dictionary Selection at Scale

The sparse dictionary coding framework represents signals as a linear combination of a few predefined dictionary atoms. It has been employed for images, time series, graph signals and recently for 2-way (or 2D) spatio-temporal data employing jointly temporal and spatial dictionaries. Large and over-complete dictionaries enable high-quality models, but also pose scalability challenges which are exacerbated in multi-dictionary settings. Hence, an important problem that we address in this paper is: How to scale multi-dictionary coding for large dictionaries and datasets? We propose a multi-dictionary atom selection technique for low-rank sparse coding named LRMDS. To enable scalability to large dictionaries and datasets, it progressively selects groups of row-column atom pairs based on their alignment with the data and performs convex relaxation coding via the corresponding sub-dictionaries. We demonstrate both theoretically and experimentally that when the data has a low-rank encoding with a sparse subset of the atoms, LRMDS is able to select them with strong guarantees under mild assumptions. Furthermore, we demonstrate the scalability and quality of LRMDS in both synthetic and real-world datasets and for a range of coding dictionaries. It achieves 3X to 10X speed-up compared to baselines, while obtaining up to two orders of magnitude improvement in representation quality on some of the real world datasets given a fixed target number of atoms.

Multi-Dictionary Tensor Decomposition

Tensor decomposition methods are popular tools for analysis of multi-way datasets from social media, healthcare, spatio-temporal domains, and others. Widely adopted models such as Tucker and canonical polyadic decomposition (CPD) follow a data-driven philosophy: they decompose a tensor into factors that approximate the observed data well. In some cases side information is available about the tensor modes. For example, in a temporal user-item purchases tensor a user influence graph, an item similarity graph, and knowledge about seasonality or trends in the temporal mode may be available. Such side information may enable more succinct and interpretable tensor decomposition models and improved quality in downstream tasks. We propose a framework for Multi-Dictionary Tensor Decomposition (MDTD) which takes advantage of prior structural information about tensor modes in the form of coding dictionaries to obtain sparsely encoded tensor factors. We derive a general optimization algorithm for MDTD that handles both complete input and input with missing values. Our framework handles large sparse tensors typical to many real-world application domains. We demonstrate MDTD's utility via experiments with both synthetic and real-world datasets. It learns more concise models than dictionary-free counterparts and improves (i) reconstruction quality ($60\%$ fewer non-zero coefficients coupled with smaller error); (ii) missing values imputation quality (two-fold MSE reduction with up to orders of magnitude time savings) and (iii) the estimation of the tensor rank. MDTD's quality improvements do not come with a running time premium: it can decompose $19GB$ datasets in less than a minute. It can also impute missing values in sparse billion-entry tensors more accurately and scalably than state-of-the-art competitors.

Temporal Graph Signal Decomposition

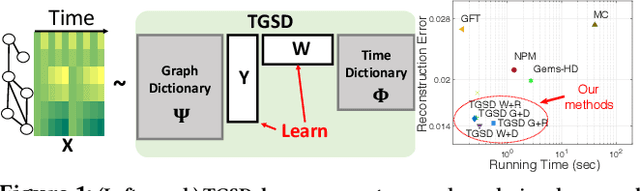
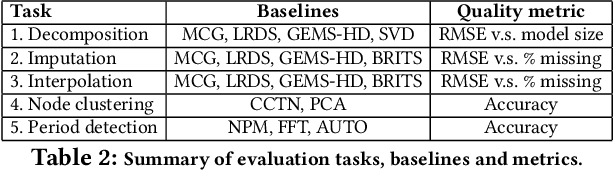
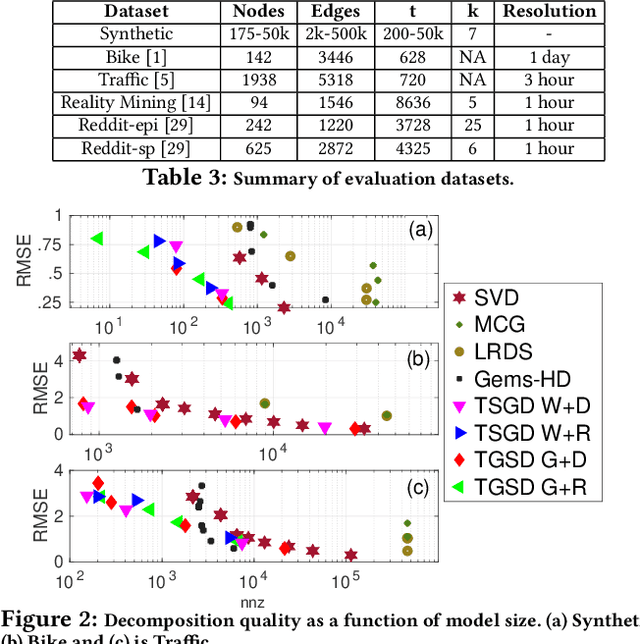
Temporal graph signals are multivariate time series with individual components associated with nodes of a fixed graph structure. Data of this kind arises in many domains including activity of social network users, sensor network readings over time, and time course gene expression within the interaction network of a model organism. Traditional matrix decomposition methods applied to such data fall short of exploiting structural regularities encoded in the underlying graph and also in the temporal patterns of the signal. How can we take into account such structure to obtain a succinct and interpretable representation of temporal graph signals? We propose a general, dictionary-based framework for temporal graph signal decomposition (TGSD). The key idea is to learn a low-rank, joint encoding of the data via a combination of graph and time dictionaries. We propose a highly scalable decomposition algorithm for both complete and incomplete data, and demonstrate its advantage for matrix decomposition, imputation of missing values, temporal interpolation, clustering, period estimation, and rank estimation in synthetic and real-world data ranging from traffic patterns to social media activity. Our framework achieves 28% reduction in RMSE compared to baselines for temporal interpolation when as many as 75% of the observations are missing. It scales best among baselines taking under 20 seconds on 3.5 million data points and produces the most parsimonious models. To the best of our knowledge, TGSD is the first framework to jointly model graph signals by temporal and graph dictionaries.