Temporal Scale Estimation for Oversampled Network Cascades: Theory, Algorithms, and Experiment
Paper and Code
Sep 22, 2021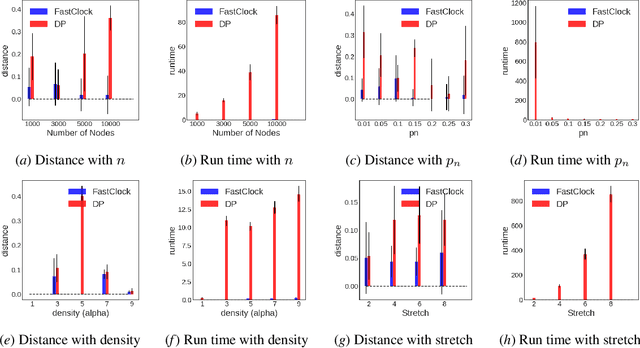
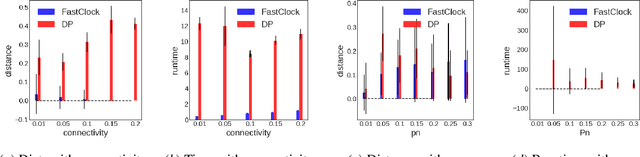
Spreading processes on graphs arise in a host of application domains, from the study of online social networks to viral marketing to epidemiology. Various discrete-time probabilistic models for spreading processes have been proposed. These are used for downstream statistical estimation and prediction problems, often involving messages or other information that is transmitted along with infections caused by the process. It is thus important to design models of cascade observation that take into account phenomena that lead to uncertainty about the process state at any given time. We highlight one such phenomenon -- temporal distortion -- caused by a misalignment between the rate at which observations of a cascade process are made and the rate at which the process itself operates, and argue that failure to correct for it results in degradation of performance on downstream statistical tasks. To address these issues, we formulate the clock estimation problem in terms of a natural distortion measure. We give a clock estimation algorithm, which we call FastClock, that runs in linear time in the size of its input and is provably statistically accurate for a broad range of model parameters when cascades are generated from the independent cascade process with known parameters and when the underlying graph is Erd\H{o}s-R\'enyi. We further give empirical results on the performance of our algorithm in comparison to the state of the art estimator, a likelihood proxy maximization-based estimator implemented via dynamic programming. We find that, in a broad parameter regime, our algorithm substantially outperforms the dynamic programming algorithm in terms of both running time and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge