Meta Flow Matching: Integrating Vector Fields on the Wasserstein Manifold

Numerous biological and physical processes can be modeled as systems of interacting entities evolving continuously over time, e.g. the dynamics of communicating cells or physical particles. Learning the dynamics of such systems is essential for predicting the temporal evolution of populations across novel samples and unseen environments. Flow-based models allow for learning these dynamics at the population level - they model the evolution of the entire distribution of samples. However, current flow-based models are limited to a single initial population and a set of predefined conditions which describe different dynamics. We argue that multiple processes in natural sciences have to be represented as vector fields on the Wasserstein manifold of probability densities. That is, the change of the population at any moment in time depends on the population itself due to the interactions between samples. In particular, this is crucial for personalized medicine where the development of diseases and their respective treatment response depends on the microenvironment of cells specific to each patient. We propose Meta Flow Matching (MFM), a practical approach to integrating along these vector fields on the Wasserstein manifold by amortizing the flow model over the initial populations. Namely, we embed the population of samples using a Graph Neural Network (GNN) and use these embeddings to train a Flow Matching model. This gives MFM the ability to generalize over the initial distributions unlike previously proposed methods. We demonstrate the ability of MFM to improve prediction of individual treatment responses on a large scale multi-patient single-cell drug screen dataset.

Investigating Generalization Behaviours of Generative Flow Networks

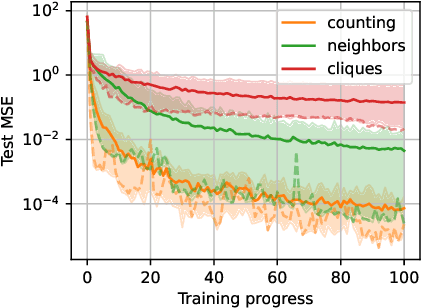
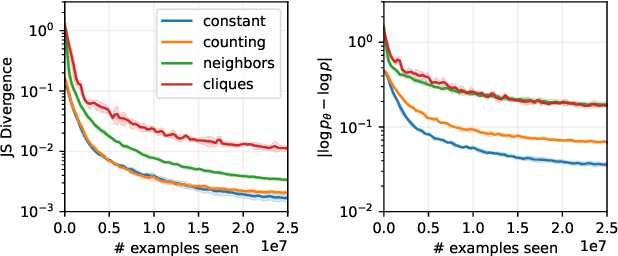
Generative Flow Networks (GFlowNets, GFNs) are a generative framework for learning unnormalized probability mass functions over discrete spaces. Since their inception, GFlowNets have proven to be useful for learning generative models in applications where the majority of the discrete space is unvisited during training. This has inspired some to hypothesize that GFlowNets, when paired with deep neural networks (DNNs), have favourable generalization properties. In this work, we empirically verify some of the hypothesized mechanisms of generalization of GFlowNets. In particular, we find that the functions that GFlowNets learn to approximate have an implicit underlying structure which facilitate generalization. We also find that GFlowNets are sensitive to being trained offline and off-policy; however, the reward implicitly learned by GFlowNets is robust to changes in the training distribution.

A Computational Framework for Solving Wasserstein Lagrangian Flows

The dynamical formulation of the optimal transport can be extended through various choices of the underlying geometry ($\textit{kinetic energy}$), and the regularization of density paths ($\textit{potential energy}$). These combinations yield different variational problems ($\textit{Lagrangians}$), encompassing many variations of the optimal transport problem such as the Schr\"odinger bridge, unbalanced optimal transport, and optimal transport with physical constraints, among others. In general, the optimal density path is unknown, and solving these variational problems can be computationally challenging. Leveraging the dual formulation of the Lagrangians, we propose a novel deep learning based framework approaching all of these problems from a unified perspective. Our method does not require simulating or backpropagating through the trajectories of the learned dynamics, and does not need access to optimal couplings. We showcase the versatility of the proposed framework by outperforming previous approaches for the single-cell trajectory inference, where incorporating prior knowledge into the dynamics is crucial for correct predictions.

Simulation-free Schrödinger bridges via score and flow matching

We present simulation-free score and flow matching ([SF]$^2$M), a simulation-free objective for inferring stochastic dynamics given unpaired source and target samples drawn from arbitrary distributions. Our method generalizes both the score-matching loss used in the training of diffusion models and the recently proposed flow matching loss used in the training of continuous normalizing flows. [SF]$^2$M interprets continuous-time stochastic generative modeling as a Schr\"odinger bridge (SB) problem. It relies on static entropy-regularized optimal transport, or a minibatch approximation, to efficiently learn the SB without simulating the learned stochastic process. We find that [SF]$^2$M is more efficient and gives more accurate solutions to the SB problem than simulation-based methods from prior work. Finally, we apply [SF]$^2$M to the problem of learning cell dynamics from snapshot data. Notably, [SF]$^2$M is the first method to accurately model cell dynamics in high dimensions and can recover known gene regulatory networks from simulated data.

DynGFN: Bayesian Dynamic Causal Discovery using Generative Flow Networks

Learning the causal structure of observable variables is a central focus for scientific discovery. Bayesian causal discovery methods tackle this problem by learning a posterior over the set of admissible graphs given our priors and observations. Existing methods primarily consider observations from static systems and assume the underlying causal structure takes the form of a directed acyclic graph (DAG). In settings with dynamic feedback mechanisms that regulate the trajectories of individual variables, this acyclicity assumption fails unless we account for time. We focus on learning Bayesian posteriors over cyclic graphs and treat causal discovery as a problem of sparse identification of a dynamical system. This imposes a natural temporal causal order between variables and captures cyclic feedback loops through time. Under this lens, we propose a new framework for Bayesian causal discovery for dynamical systems and present a novel generative flow network architecture (DynGFN) tailored for this task. Our results indicate that DynGFN learns posteriors that better encapsulate the distributions over admissible cyclic causal structures compared to counterpart state-of-the-art approaches.