Simplifying Neural Network Training Under Class Imbalance

Real-world datasets are often highly class-imbalanced, which can adversely impact the performance of deep learning models. The majority of research on training neural networks under class imbalance has focused on specialized loss functions, sampling techniques, or two-stage training procedures. Notably, we demonstrate that simply tuning existing components of standard deep learning pipelines, such as the batch size, data augmentation, optimizer, and label smoothing, can achieve state-of-the-art performance without any such specialized class imbalance methods. We also provide key prescriptions and considerations for training under class imbalance, and an understanding of why imbalance methods succeed or fail.

A Study of Bayesian Neural Network Surrogates for Bayesian Optimization

Bayesian optimization is a highly efficient approach to optimizing objective functions which are expensive to query. These objectives are typically represented by Gaussian process (GP) surrogate models which are easy to optimize and support exact inference. While standard GP surrogates have been well-established in Bayesian optimization, Bayesian neural networks (BNNs) have recently become practical function approximators, with many benefits over standard GPs such as the ability to naturally handle non-stationarity and learn representations for high-dimensional data. In this paper, we study BNNs as alternatives to standard GP surrogates for optimization. We consider a variety of approximate inference procedures for finite-width BNNs, including high-quality Hamiltonian Monte Carlo, low-cost stochastic MCMC, and heuristics such as deep ensembles. We also consider infinite-width BNNs and partially stochastic models such as deep kernel learning. We evaluate this collection of surrogate models on diverse problems with varying dimensionality, number of objectives, non-stationarity, and discrete and continuous inputs. We find: (i) the ranking of methods is highly problem dependent, suggesting the need for tailored inductive biases; (ii) HMC is the most successful approximate inference procedure for fully stochastic BNNs; (iii) full stochasticity may be unnecessary as deep kernel learning is relatively competitive; (iv) infinite-width BNNs are particularly promising, especially in high dimensions.

PPL Bench: Evaluation Framework For Probabilistic Programming Languages

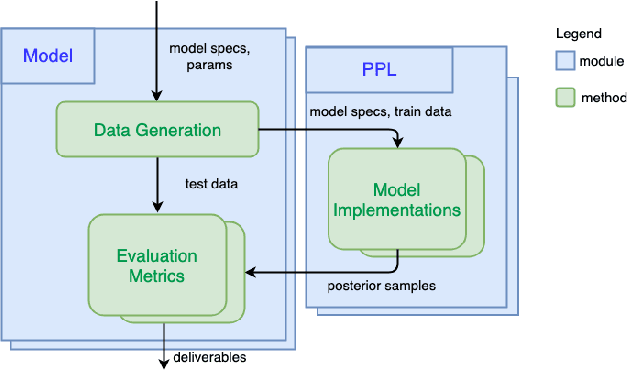
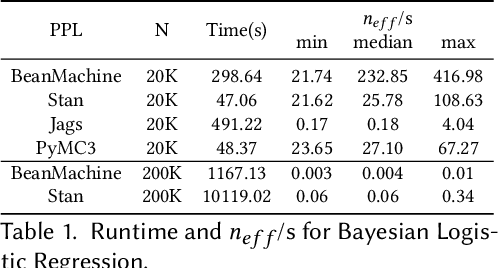
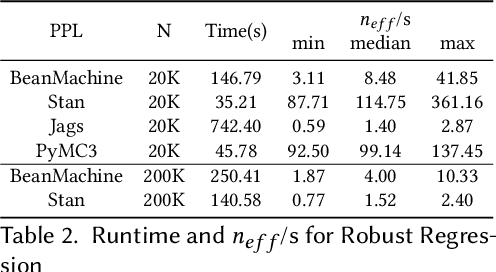
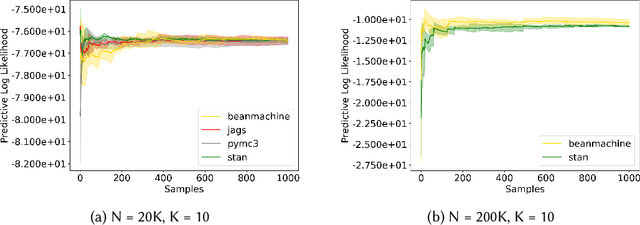
We introduce PPL Bench, a new benchmark for evaluating Probabilistic Programming Languages (PPLs) on a variety of statistical models. The benchmark includes data generation and evaluation code for a number of models as well as implementations in some common PPLs. All of the benchmark code and PPL implementations are available on Github. We welcome contributions of new models and PPLs and as well as improvements in existing PPL implementations. The purpose of the benchmark is two-fold. First, we want researchers as well as conference reviewers to be able to evaluate improvements in PPLs in a standardized setting. Second, we want end users to be able to pick the PPL that is most suited for their modeling application. In particular, we are interested in evaluating the accuracy and speed of convergence of the inferred posterior. Each PPL only needs to provide posterior samples given a model and observation data. The framework automatically computes and plots growth in predictive log-likelihood on held out data in addition to reporting other common metrics such as effective sample size and $\hat{r}$.

Newtonian Monte Carlo: single-site MCMC meets second-order gradient methods

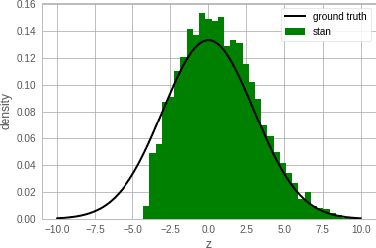
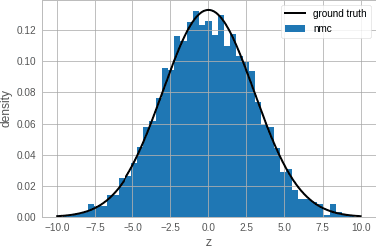
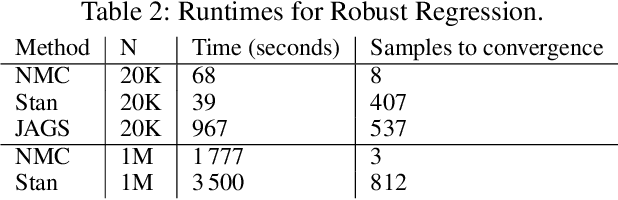
Single-site Markov Chain Monte Carlo (MCMC) is a variant of MCMC in which a single coordinate in the state space is modified in each step. Structured relational models are a good candidate for this style of inference. In the single-site context, second order methods become feasible because the typical cubic costs associated with these methods is now restricted to the dimension of each coordinate. Our work, which we call Newtonian Monte Carlo (NMC), is a method to improve MCMC convergence by analyzing the first and second order gradients of the target density to determine a suitable proposal density at each point. Existing first order gradient-based methods suffer from the problem of determining an appropriate step size. Too small a step size and it will take a large number of steps to converge, while a very large step size will cause it to overshoot the high density region. NMC is similar to the Newton-Raphson update in optimization where the second order gradient is used to automatically scale the step size in each dimension. However, our objective is to find a parameterized proposal density rather than the maxima. As a further improvement on existing first and second order methods, we show that random variables with constrained supports don't need to be transformed before taking a gradient step. We demonstrate the efficiency of NMC on a number of different domains. For statistical models where the prior is conjugate to the likelihood, our method recovers the posterior quite trivially in one step. However, we also show results on fairly large non-conjugate models, where NMC performs better than adaptive first order methods such as NUTS or other inexact scalable inference methods such as Stochastic Variational Inference or bootstrapping.