Preemptive Detection of Fake Accounts on Social Networks via Multi-Class Preferential Attachment Classifiers

In this paper, we describe a new algorithm called Preferential Attachment k-class Classifier (PreAttacK) for detecting fake accounts in a social network. Recently, several algorithms have obtained high accuracy on this problem. However, they have done so by relying on information about fake accounts' friendships or the content they share with others--the very things we seek to prevent. PreAttacK represents a significant departure from these approaches. We provide some of the first detailed distributional analyses of how new fake (and real) accounts first attempt to request friends after joining a major network (Facebook). We show that even before a new account has made friends or shared content, these initial friend request behaviors evoke a natural multi-class extension of the canonical Preferential Attachment model of social network growth. We use this model to derive a new algorithm, PreAttacK. We prove that in relevant problem instances, PreAttacK near-optimally approximates the posterior probability that a new account is fake under this multi-class Preferential Attachment model of new accounts' (not-yet-answered) friend requests. These are the first provable guarantees for fake account detection that apply to new users, and that do not require strong homophily assumptions. This principled approach also makes PreAttacK the only algorithm with provable guarantees that obtains state-of-the-art performance on new users on the global Facebook network, where it converges to AUC=0.9 after new users send + receive a total of just 20 not-yet-answered friend requests. For comparison, state-of-the-art benchmarks do not obtain this AUC even after observing additional data on new users' first 100 friend requests. Thus, unlike mainstream algorithms, PreAttacK converges before the median new fake account has made a single friendship (accepted friend request) with a human.

Accelerating Metropolis-Hastings with Lightweight Inference Compilation

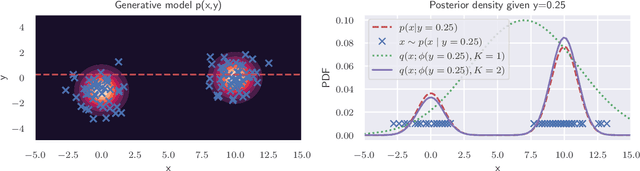
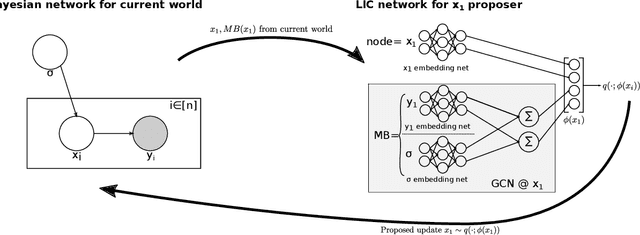
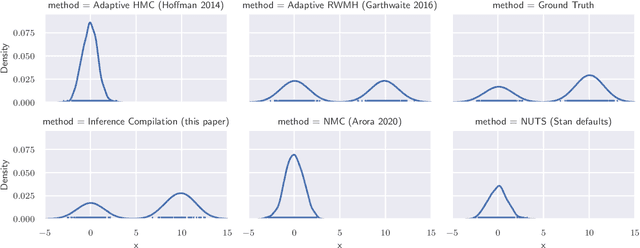
In order to construct accurate proposers for Metropolis-Hastings Markov Chain Monte Carlo, we integrate ideas from probabilistic graphical models and neural networks in an open-source framework we call Lightweight Inference Compilation (LIC). LIC implements amortized inference within an open-universe declarative probabilistic programming language (PPL). Graph neural networks are used to parameterize proposal distributions as functions of Markov blankets, which during "compilation" are optimized to approximate single-site Gibbs sampling distributions. Unlike prior work in inference compilation (IC), LIC forgoes importance sampling of linear execution traces in favor of operating directly on Bayesian networks. Through using a declarative PPL, the Markov blankets of nodes (which may be non-static) are queried at inference-time to produce proposers Experimental results show LIC can produce proposers which have less parameters, greater robustness to nuisance random variables, and improved posterior sampling in a Bayesian logistic regression and $n$-schools inference application.

PPL Bench: Evaluation Framework For Probabilistic Programming Languages

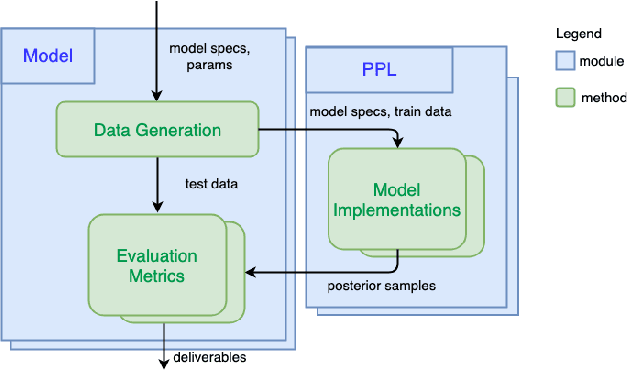
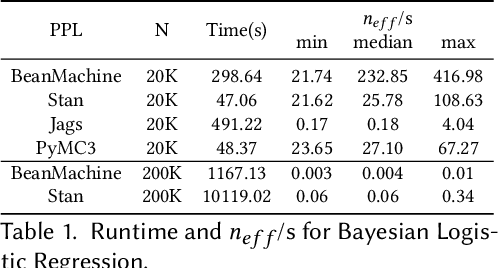
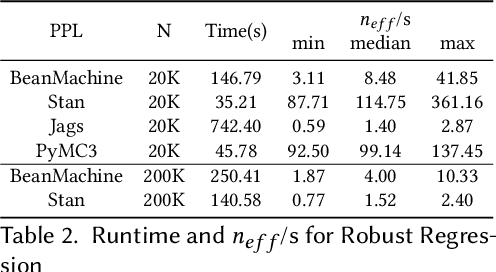
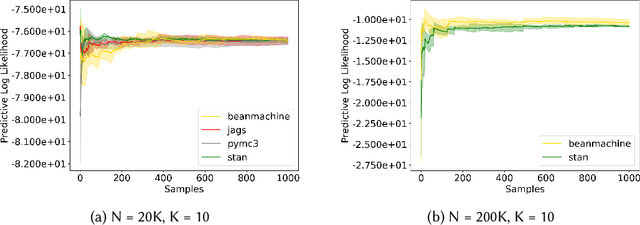
We introduce PPL Bench, a new benchmark for evaluating Probabilistic Programming Languages (PPLs) on a variety of statistical models. The benchmark includes data generation and evaluation code for a number of models as well as implementations in some common PPLs. All of the benchmark code and PPL implementations are available on Github. We welcome contributions of new models and PPLs and as well as improvements in existing PPL implementations. The purpose of the benchmark is two-fold. First, we want researchers as well as conference reviewers to be able to evaluate improvements in PPLs in a standardized setting. Second, we want end users to be able to pick the PPL that is most suited for their modeling application. In particular, we are interested in evaluating the accuracy and speed of convergence of the inferred posterior. Each PPL only needs to provide posterior samples given a model and observation data. The framework automatically computes and plots growth in predictive log-likelihood on held out data in addition to reporting other common metrics such as effective sample size and $\hat{r}$.

Uncertainty Estimation For Community Standards Violation In Online Social Networks

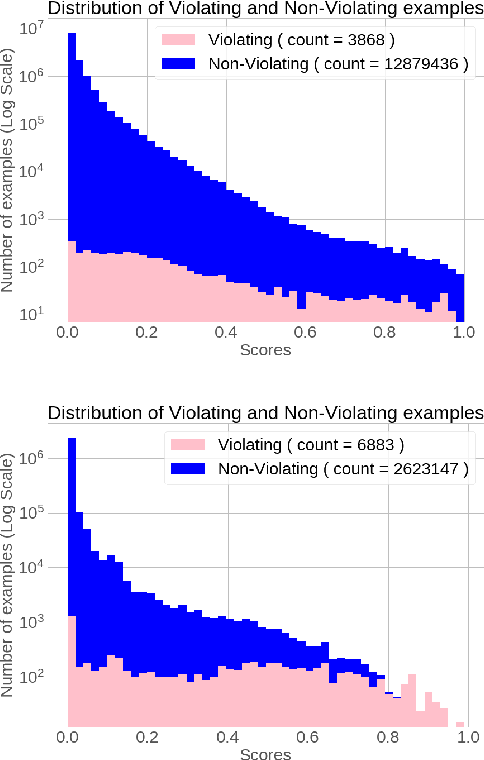
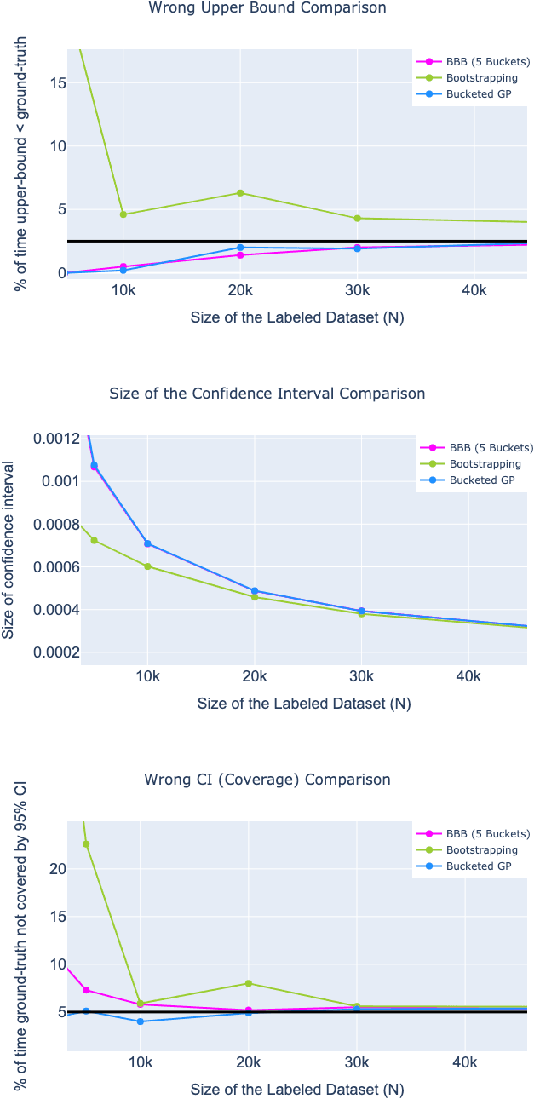
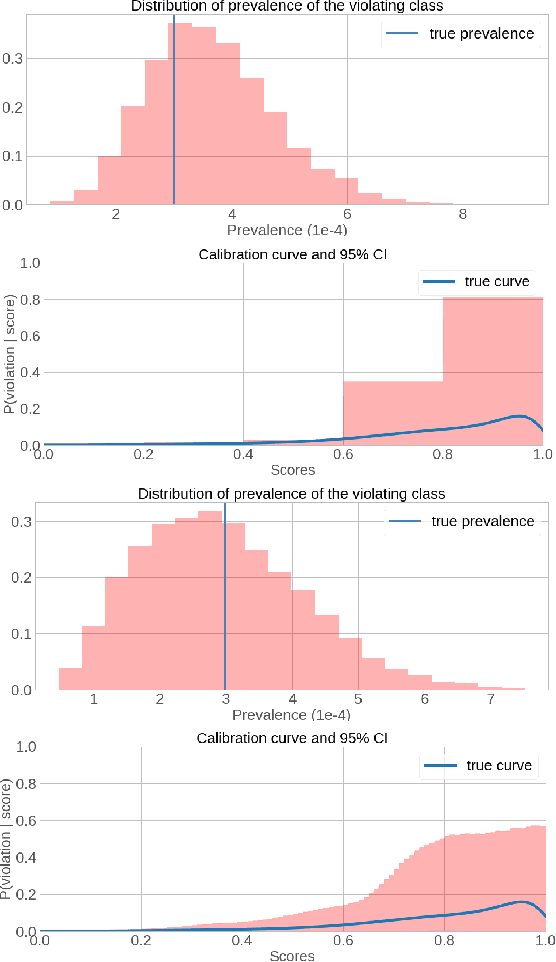
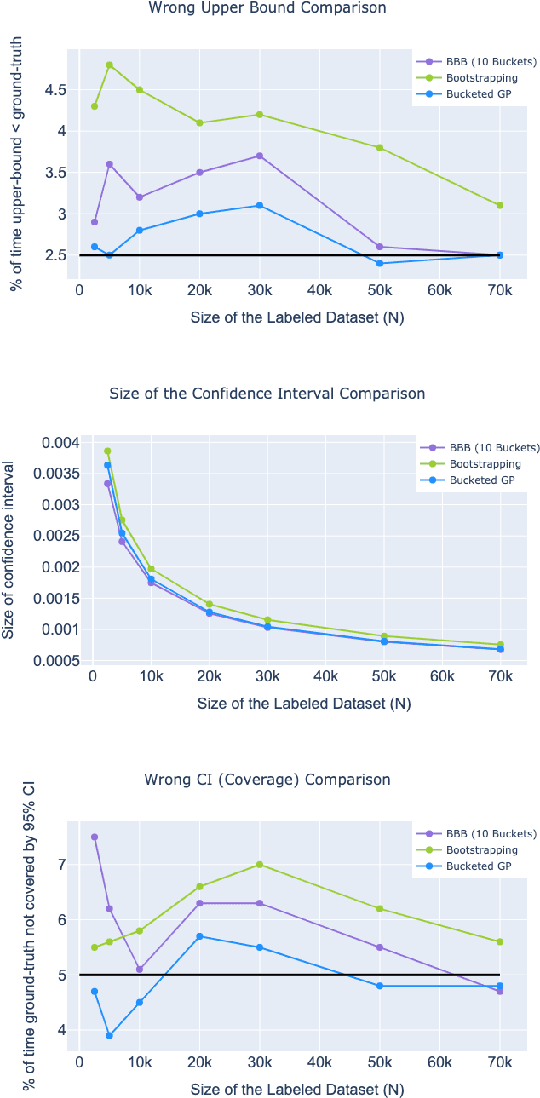
Online Social Networks (OSNs) provide a platform for users to share their thoughts and opinions with their community of friends or to the general public. In order to keep the platform safe for all users, as well as to keep it compliant with local laws, OSNs typically create a set of community standards organized into policy groups, and use Machine Learning (ML) models to identify and remove content that violates any of the policies. However, out of the billions of content that is uploaded on a daily basis only a small fraction is so unambiguously violating that it can be removed by the automated models. Prevalence estimation is the task of estimating the fraction of violating content in the residual items by sending a small sample of these items to human labelers to get ground truth labels. This task is exceedingly hard because even though we can easily get the ML scores or features for all of the billions of items we can only get ground truth labels on a few thousands of these items due to practical considerations. Indeed the prevalence can be so low that even after a judicious choice of items to be labeled there can be many days in which not even a single item is labeled violating. A pragmatic choice for such low prevalence, $10^{-4}$ to $10^{-5}$, regimes is to report the upper bound, or $97.5\%$ confidence interval, prevalence (UBP) that takes the uncertainties of the sampling and labeling processes into account and gives a smoothed estimate. In this work we present two novel techniques Bucketed-Beta-Binomial and a Bucketed-Gaussian Process for this UBP task and demonstrate on real and simulated data that it has much better coverage than the commonly used bootstrapping technique.

Newtonian Monte Carlo: single-site MCMC meets second-order gradient methods

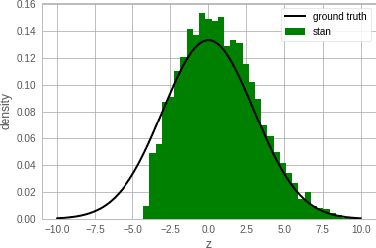
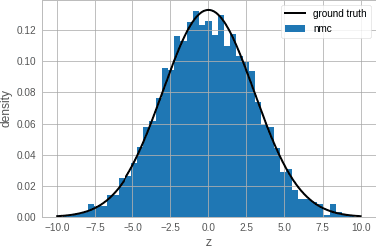
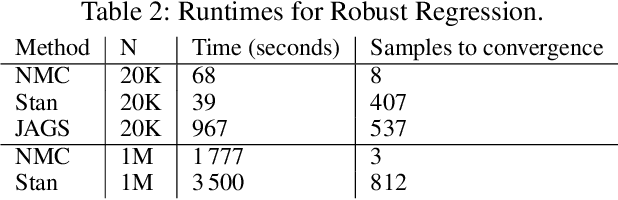
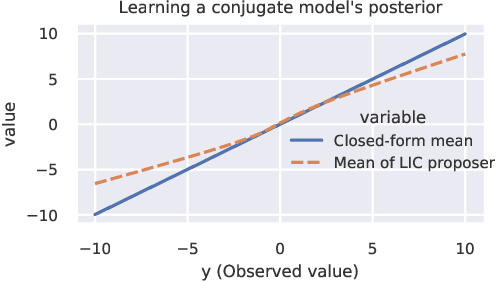
Single-site Markov Chain Monte Carlo (MCMC) is a variant of MCMC in which a single coordinate in the state space is modified in each step. Structured relational models are a good candidate for this style of inference. In the single-site context, second order methods become feasible because the typical cubic costs associated with these methods is now restricted to the dimension of each coordinate. Our work, which we call Newtonian Monte Carlo (NMC), is a method to improve MCMC convergence by analyzing the first and second order gradients of the target density to determine a suitable proposal density at each point. Existing first order gradient-based methods suffer from the problem of determining an appropriate step size. Too small a step size and it will take a large number of steps to converge, while a very large step size will cause it to overshoot the high density region. NMC is similar to the Newton-Raphson update in optimization where the second order gradient is used to automatically scale the step size in each dimension. However, our objective is to find a parameterized proposal density rather than the maxima. As a further improvement on existing first and second order methods, we show that random variables with constrained supports don't need to be transformed before taking a gradient step. We demonstrate the efficiency of NMC on a number of different domains. For statistical models where the prior is conjugate to the likelihood, our method recovers the posterior quite trivially in one step. However, we also show results on fairly large non-conjugate models, where NMC performs better than adaptive first order methods such as NUTS or other inexact scalable inference methods such as Stochastic Variational Inference or bootstrapping.