Hardware-accelerated Simulation-based Inference of Stochastic Epidemiology Models for COVID-19

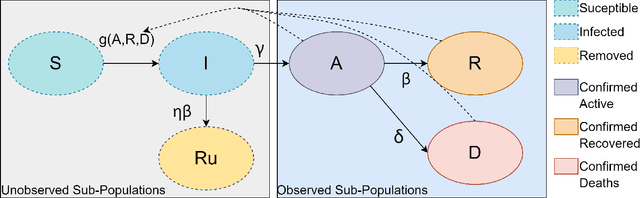
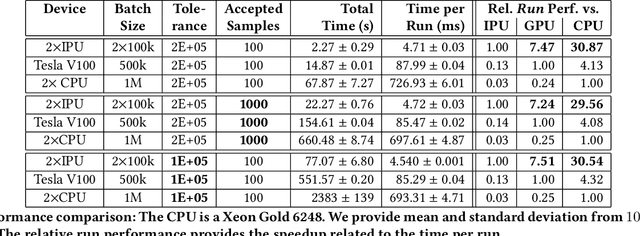
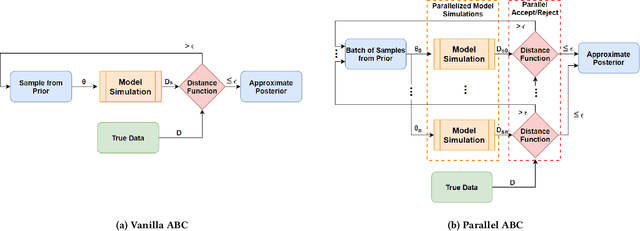
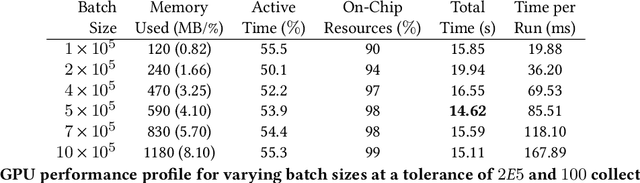
Epidemiology models are central in understanding and controlling large scale pandemics. Several epidemiology models require simulation-based inference such as Approximate Bayesian Computation (ABC) to fit their parameters to observations. ABC inference is highly amenable to efficient hardware acceleration. In this work, we develop parallel ABC inference of a stochastic epidemiology model for COVID-19. The statistical inference framework is implemented and compared on Intel Xeon CPU, NVIDIA Tesla V100 GPU and the Graphcore Mk1 IPU, and the results are discussed in the context of their computational architectures. Results show that GPUs are 4x and IPUs are 30x faster than Xeon CPUs. Extensive performance analysis indicates that the difference between IPU and GPU can be attributed to higher communication bandwidth, closeness of memory to compute, and higher compute power in the IPU. The proposed framework scales across 16 IPUs, with scaling overhead not exceeding 8% for the experiments performed. We present an example of our framework in practice, performing inference on the epidemiology model across three countries, and giving a brief overview of the results.

PPL Bench: Evaluation Framework For Probabilistic Programming Languages

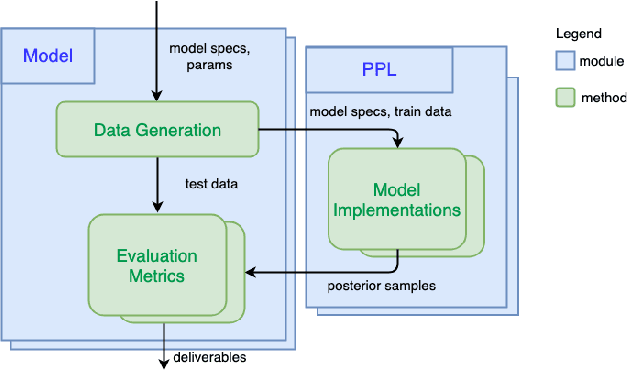
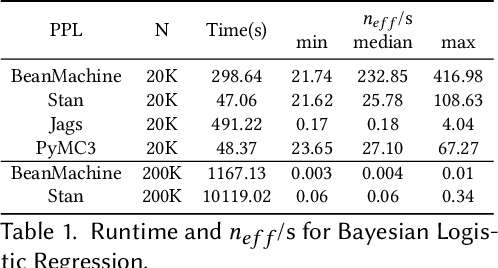
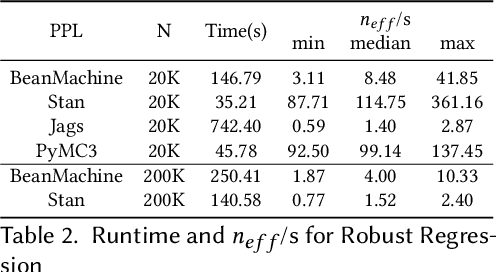
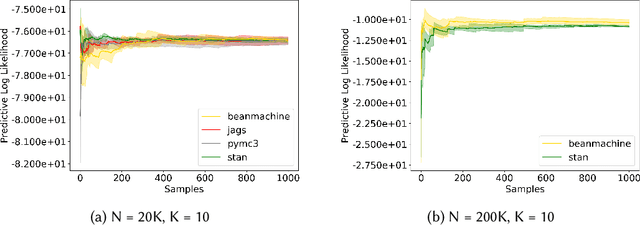
We introduce PPL Bench, a new benchmark for evaluating Probabilistic Programming Languages (PPLs) on a variety of statistical models. The benchmark includes data generation and evaluation code for a number of models as well as implementations in some common PPLs. All of the benchmark code and PPL implementations are available on Github. We welcome contributions of new models and PPLs and as well as improvements in existing PPL implementations. The purpose of the benchmark is two-fold. First, we want researchers as well as conference reviewers to be able to evaluate improvements in PPLs in a standardized setting. Second, we want end users to be able to pick the PPL that is most suited for their modeling application. In particular, we are interested in evaluating the accuracy and speed of convergence of the inferred posterior. Each PPL only needs to provide posterior samples given a model and observation data. The framework automatically computes and plots growth in predictive log-likelihood on held out data in addition to reporting other common metrics such as effective sample size and $\hat{r}$.