Uncertainty Estimation For Community Standards Violation In Online Social Networks

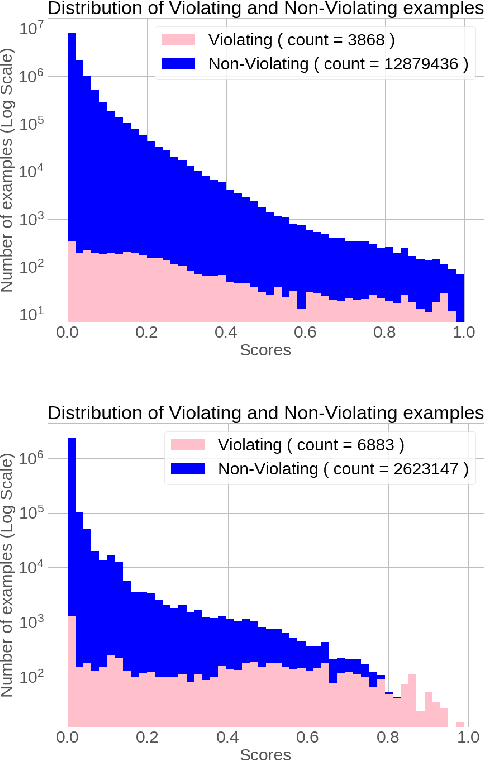
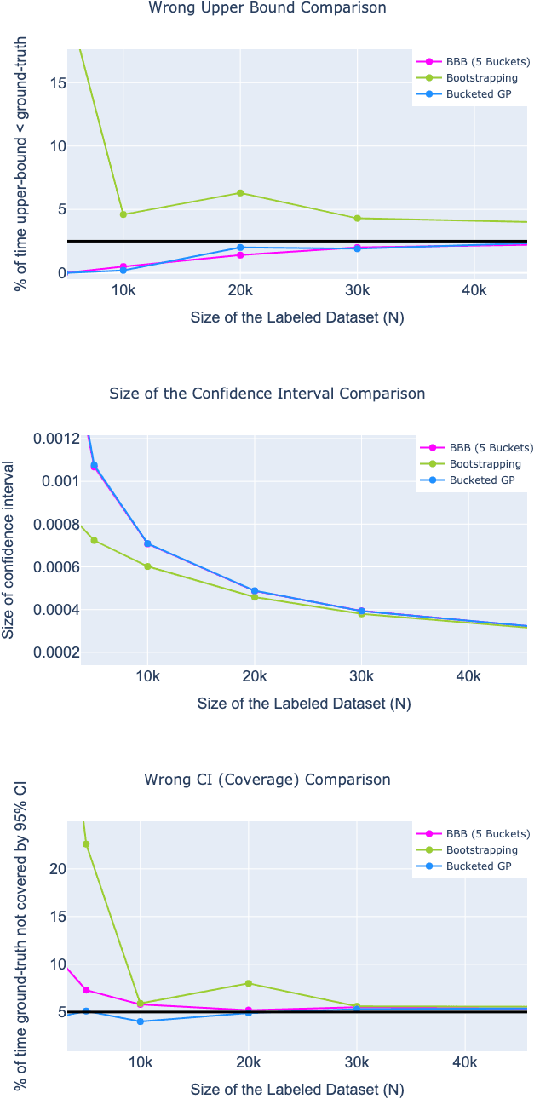
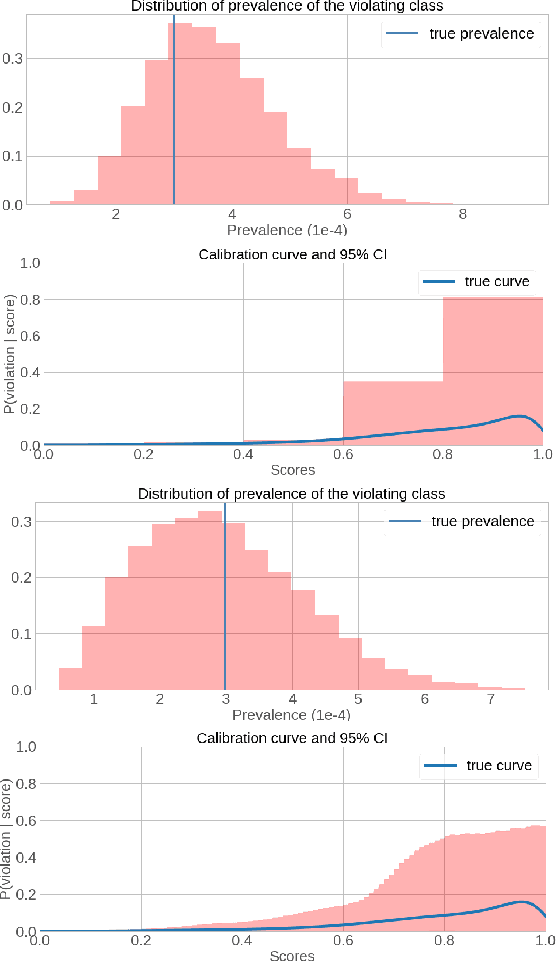
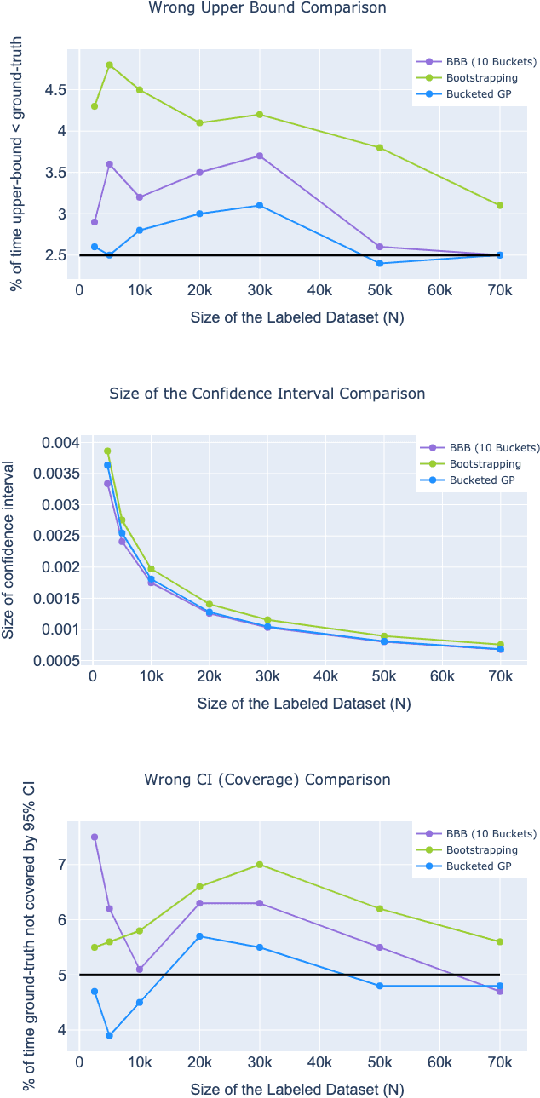
Online Social Networks (OSNs) provide a platform for users to share their thoughts and opinions with their community of friends or to the general public. In order to keep the platform safe for all users, as well as to keep it compliant with local laws, OSNs typically create a set of community standards organized into policy groups, and use Machine Learning (ML) models to identify and remove content that violates any of the policies. However, out of the billions of content that is uploaded on a daily basis only a small fraction is so unambiguously violating that it can be removed by the automated models. Prevalence estimation is the task of estimating the fraction of violating content in the residual items by sending a small sample of these items to human labelers to get ground truth labels. This task is exceedingly hard because even though we can easily get the ML scores or features for all of the billions of items we can only get ground truth labels on a few thousands of these items due to practical considerations. Indeed the prevalence can be so low that even after a judicious choice of items to be labeled there can be many days in which not even a single item is labeled violating. A pragmatic choice for such low prevalence, $10^{-4}$ to $10^{-5}$, regimes is to report the upper bound, or $97.5\%$ confidence interval, prevalence (UBP) that takes the uncertainties of the sampling and labeling processes into account and gives a smoothed estimate. In this work we present two novel techniques Bucketed-Beta-Binomial and a Bucketed-Gaussian Process for this UBP task and demonstrate on real and simulated data that it has much better coverage than the commonly used bootstrapping technique.

Newtonian Monte Carlo: single-site MCMC meets second-order gradient methods

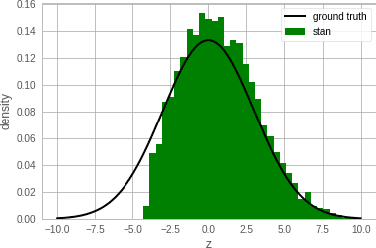
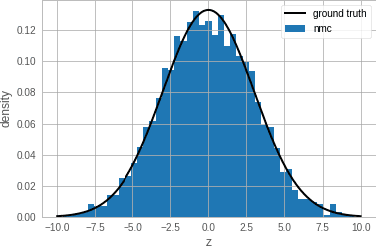
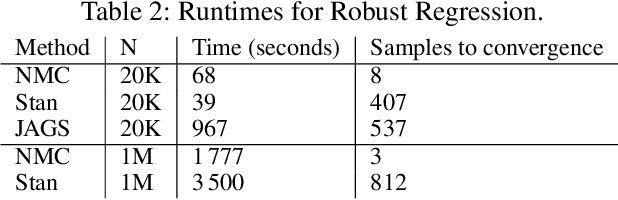
Single-site Markov Chain Monte Carlo (MCMC) is a variant of MCMC in which a single coordinate in the state space is modified in each step. Structured relational models are a good candidate for this style of inference. In the single-site context, second order methods become feasible because the typical cubic costs associated with these methods is now restricted to the dimension of each coordinate. Our work, which we call Newtonian Monte Carlo (NMC), is a method to improve MCMC convergence by analyzing the first and second order gradients of the target density to determine a suitable proposal density at each point. Existing first order gradient-based methods suffer from the problem of determining an appropriate step size. Too small a step size and it will take a large number of steps to converge, while a very large step size will cause it to overshoot the high density region. NMC is similar to the Newton-Raphson update in optimization where the second order gradient is used to automatically scale the step size in each dimension. However, our objective is to find a parameterized proposal density rather than the maxima. As a further improvement on existing first and second order methods, we show that random variables with constrained supports don't need to be transformed before taking a gradient step. We demonstrate the efficiency of NMC on a number of different domains. For statistical models where the prior is conjugate to the likelihood, our method recovers the posterior quite trivially in one step. However, we also show results on fairly large non-conjugate models, where NMC performs better than adaptive first order methods such as NUTS or other inexact scalable inference methods such as Stochastic Variational Inference or bootstrapping.

Gibbs Sampling in Open-Universe Stochastic Languages

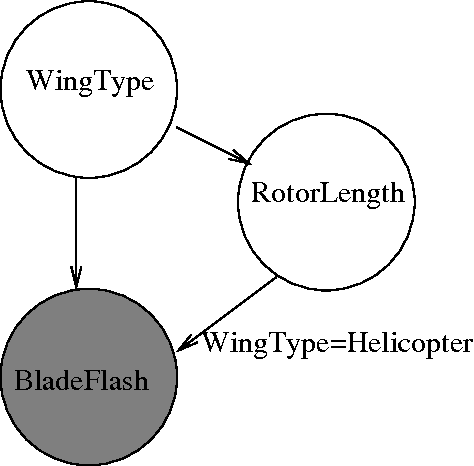
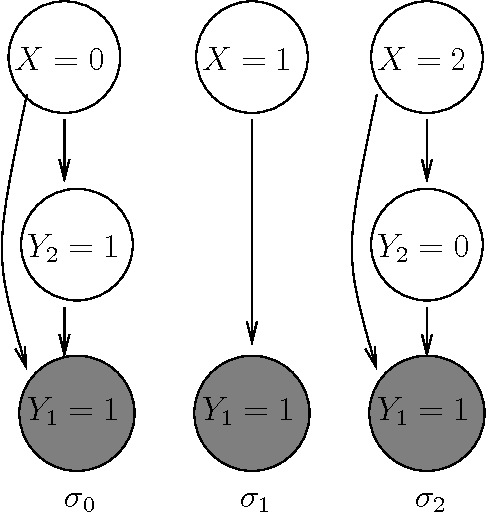
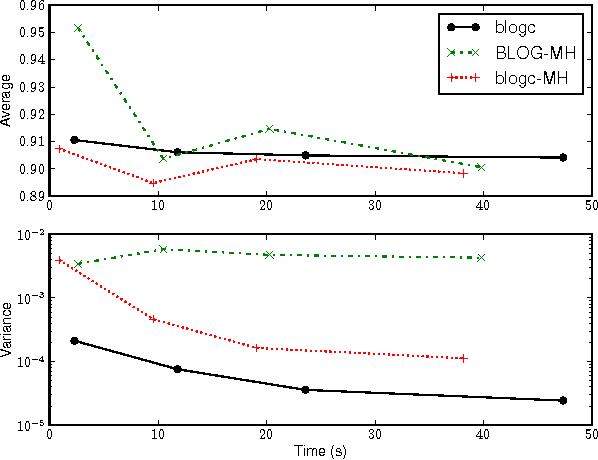
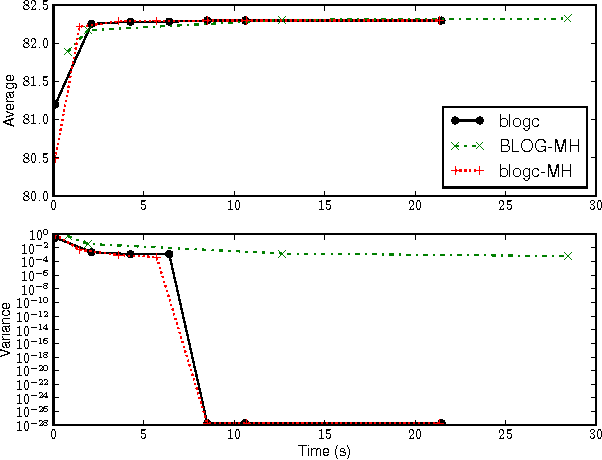
Languages for open-universe probabilistic models (OUPMs) can represent situations with an unknown number of objects and iden- tity uncertainty. While such cases arise in a wide range of important real-world appli- cations, existing general purpose inference methods for OUPMs are far less efficient than those available for more restricted lan- guages and model classes. This paper goes some way to remedying this deficit by in- troducing, and proving correct, a generaliza- tion of Gibbs sampling to partial worlds with possibly varying model structure. Our ap- proach draws on and extends previous generic OUPM inference methods, as well as aux- iliary variable samplers for nonparametric mixture models. It has been implemented for BLOG, a well-known OUPM language. Combined with compile-time optimizations, the resulting algorithm yields very substan- tial speedups over existing methods on sev- eral test cases, and substantially improves the practicality of OUPM languages generally.