Pearl: A Production-ready Reinforcement Learning Agent

Reinforcement Learning (RL) offers a versatile framework for achieving long-term goals. Its generality allows us to formalize a wide range of problems that real-world intelligent systems encounter, such as dealing with delayed rewards, handling partial observability, addressing the exploration and exploitation dilemma, utilizing offline data to improve online performance, and ensuring safety constraints are met. Despite considerable progress made by the RL research community in addressing these issues, existing open-source RL libraries tend to focus on a narrow portion of the RL solution pipeline, leaving other aspects largely unattended. This paper introduces Pearl, a Production-ready RL agent software package explicitly designed to embrace these challenges in a modular fashion. In addition to presenting preliminary benchmark results, this paper highlights Pearl's industry adoptions to demonstrate its readiness for production usage. Pearl is open sourced on Github at github.com/facebookresearch/pearl and its official website is located at pearlagent.github.io.

Exact Inference for Relational Graphical Models with Interpreted Functions: Lifted Probabilistic Inference Modulo Theories

Probabilistic Inference Modulo Theories (PIMT) is a recent framework that expands exact inference on graphical models to use richer languages that include arithmetic, equalities, and inequalities on both integers and real numbers. In this paper, we expand PIMT to a lifted version that also processes random functions and relations. This enhancement is achieved by adapting Inversion, a method from Lifted First-Order Probabilistic Inference literature, to also be modulo theories. This results in the first algorithm for exact probabilistic inference that efficiently and simultaneously exploits random relations and functions, arithmetic, equalities and inequalities.

Anytime Exact Belief Propagation

Statistical Relational Models and, more recently, Probabilistic Programming, have been making strides towards an integration of logic and probabilistic reasoning. A natural expectation for this project is that a probabilistic logic reasoning algorithm reduces to a logic reasoning algorithm when provided a model that only involves 0-1 probabilities, exhibiting all the advantages of logic reasoning such as short-circuiting, intelligibility, and the ability to provide proof trees for a query answer. In fact, we can take this further and require that these characteristics be present even for probabilistic models with probabilities \emph{near} 0 and 1, with graceful degradation as the model becomes more uncertain. We also seek inference that has amortized constant time complexity on a model's size (even if still exponential in the induced width of a more directly relevant portion of it) so that it can be applied to huge knowledge bases of which only a relatively small portion is relevant to typical queries. We believe that, among the probabilistic reasoning algorithms, Belief Propagation is the most similar to logic reasoning: messages are propagated among neighboring variables, and the paths of message-passing are similar to proof trees. However, Belief Propagation is either only applicable to tree models, or approximate (and without guarantees) for precision and convergence. In this paper we present work in progress on an Anytime Exact Belief Propagation algorithm that is very similar to Belief Propagation but is exact even for graphical models with cycles, while exhibiting soft short-circuiting, amortized constant time complexity in the model size, and which can provide probabilistic proof trees.

Probabilistic Inference Modulo Theories

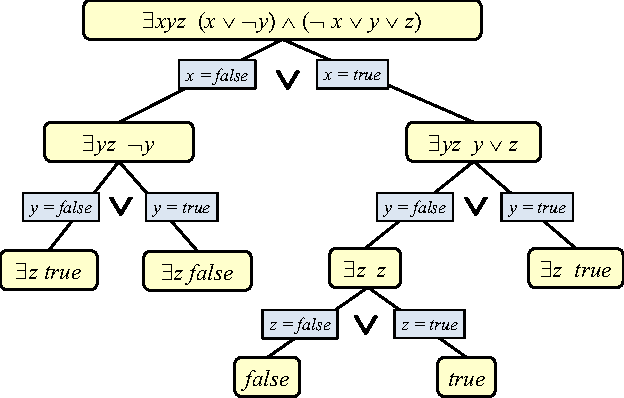
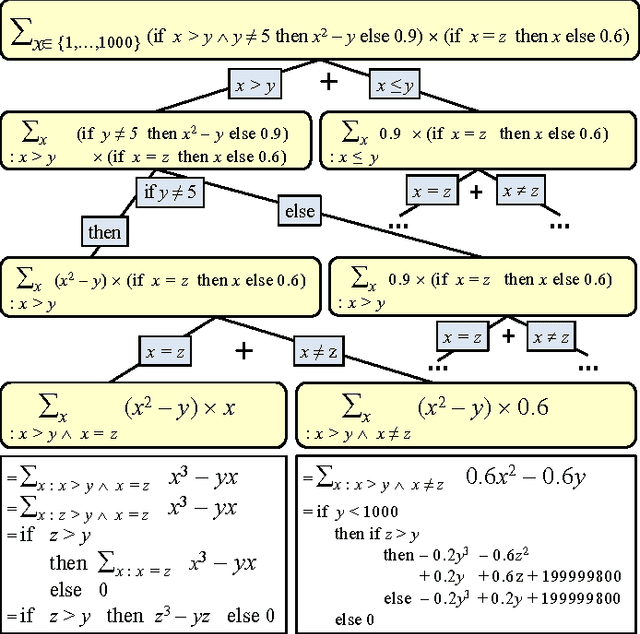
We present SGDPLL(T), an algorithm that solves (among many other problems) probabilistic inference modulo theories, that is, inference problems over probabilistic models defined via a logic theory provided as a parameter (currently, propositional, equalities on discrete sorts, and inequalities, more specifically difference arithmetic, on bounded integers). While many solutions to probabilistic inference over logic representations have been proposed, SGDPLL(T) is simultaneously (1) lifted, (2) exact and (3) modulo theories, that is, parameterized by a background logic theory. This offers a foundation for extending it to rich logic languages such as data structures and relational data. By lifted, we mean algorithms with constant complexity in the domain size (the number of values that variables can take). We also detail a solver for summations with difference arithmetic and show experimental results from a scenario in which SGDPLL(T) is much faster than a state-of-the-art probabilistic solver.

Gibbs Sampling in Open-Universe Stochastic Languages

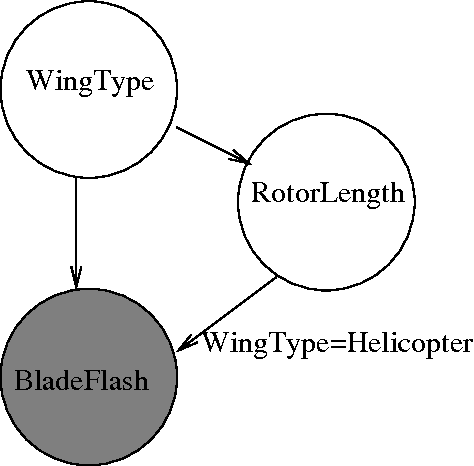
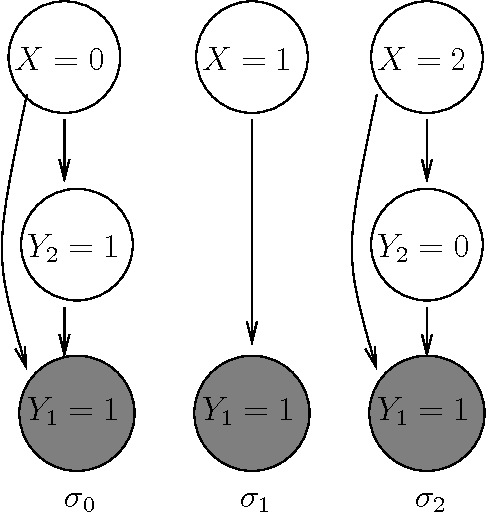
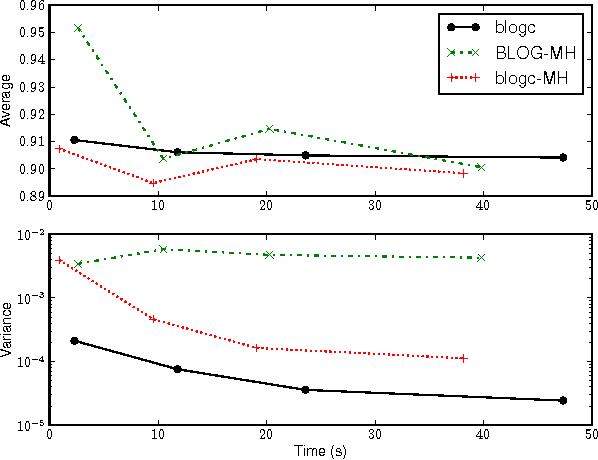
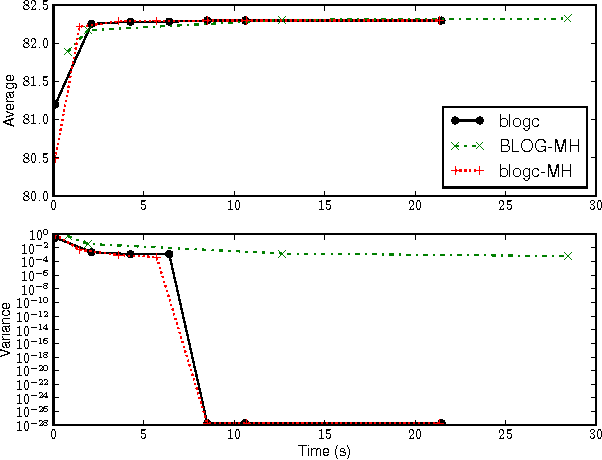
Languages for open-universe probabilistic models (OUPMs) can represent situations with an unknown number of objects and iden- tity uncertainty. While such cases arise in a wide range of important real-world appli- cations, existing general purpose inference methods for OUPMs are far less efficient than those available for more restricted lan- guages and model classes. This paper goes some way to remedying this deficit by in- troducing, and proving correct, a generaliza- tion of Gibbs sampling to partial worlds with possibly varying model structure. Our ap- proach draws on and extends previous generic OUPM inference methods, as well as aux- iliary variable samplers for nonparametric mixture models. It has been implemented for BLOG, a well-known OUPM language. Combined with compile-time optimizations, the resulting algorithm yields very substan- tial speedups over existing methods on sev- eral test cases, and substantially improves the practicality of OUPM languages generally.