Can Transformers Learn Full Bayesian Inference in Context?

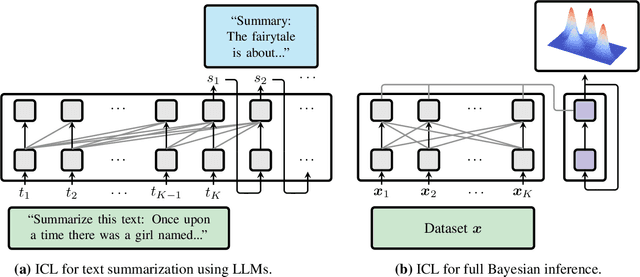
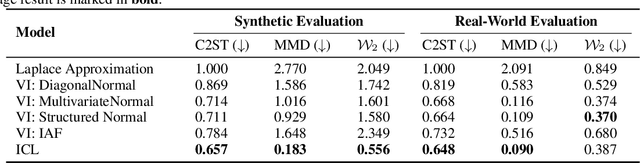
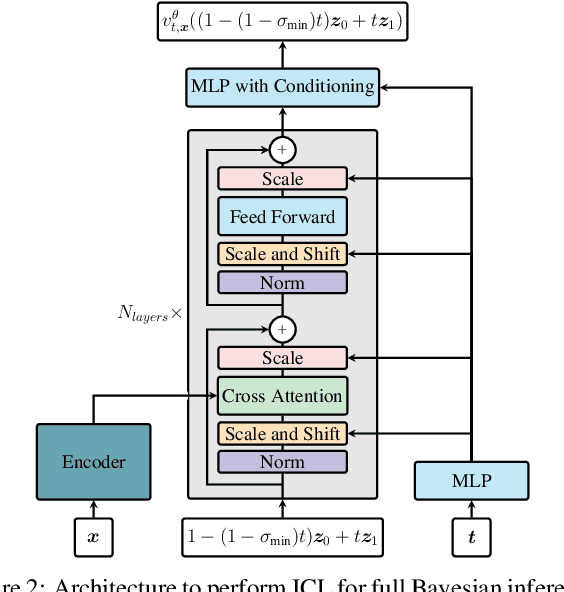
Transformers have emerged as the dominant architecture in the field of deep learning, with a broad range of applications and remarkable in-context learning (ICL) capabilities. While not yet fully understood, ICL has already proved to be an intriguing phenomenon, allowing transformers to learn in context -- without requiring further training. In this paper, we further advance the understanding of ICL by demonstrating that transformers can perform full Bayesian inference for commonly used statistical models in context. More specifically, we introduce a general framework that builds on ideas from prior fitted networks and continuous normalizing flows which enables us to infer complex posterior distributions for methods such as generalized linear models and latent factor models. Extensive experiments on real-world datasets demonstrate that our ICL approach yields posterior samples that are similar in quality to state-of-the-art MCMC or variational inference methods not operating in context.