Conformal Validity Guarantees Exist for Any Data Distribution
Paper and Code
May 10, 2024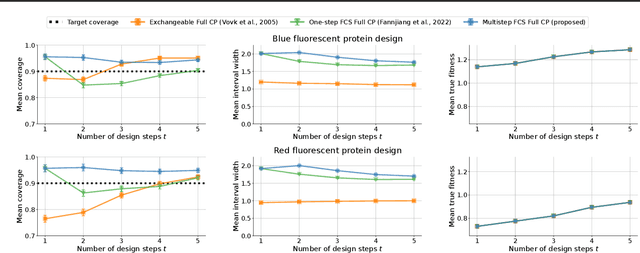
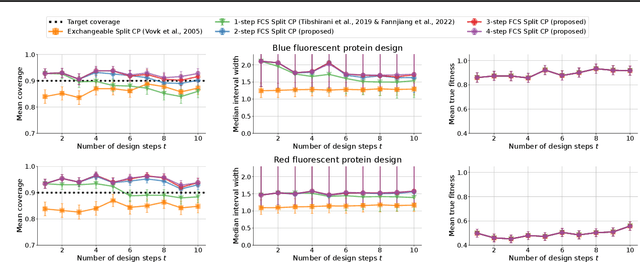
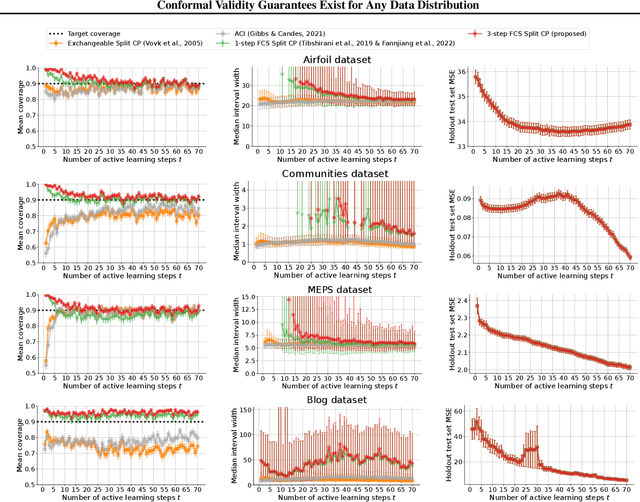
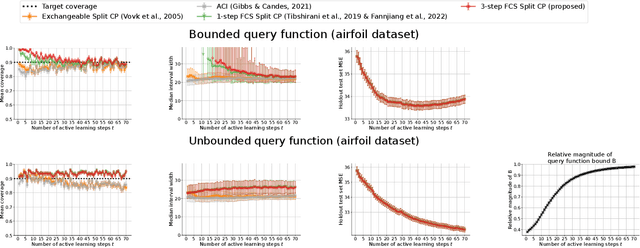
As machine learning (ML) gains widespread adoption, practitioners are increasingly seeking means to quantify and control the risk these systems incur. This challenge is especially salient when ML systems have autonomy to collect their own data, such as in black-box optimization and active learning, where their actions induce sequential feedback-loop shifts in the data distribution. Conformal prediction has emerged as a promising approach to uncertainty and risk quantification, but existing variants either fail to accommodate sequences of data-dependent shifts, or do not fully exploit the fact that agent-induced shift is under our control. In this work we prove that conformal prediction can theoretically be extended to \textit{any} joint data distribution, not just exchangeable or quasi-exchangeable ones, although it is exceedingly impractical to compute in the most general case. For practical applications, we outline a procedure for deriving specific conformal algorithms for any data distribution, and we use this procedure to derive tractable algorithms for a series of agent-induced covariate shifts. We evaluate the proposed algorithms empirically on synthetic black-box optimization and active learning tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge