Is novelty predictable?

Machine learning-based design has gained traction in the sciences, most notably in the design of small molecules, materials, and proteins, with societal implications spanning drug development and manufacturing, plastic degradation, and carbon sequestration. When designing objects to achieve novel property values with machine learning, one faces a fundamental challenge: how to push past the frontier of current knowledge, distilled from the training data into the model, in a manner that rationally controls the risk of failure. If one trusts learned models too much in extrapolation, one is likely to design rubbish. In contrast, if one does not extrapolate, one cannot find novelty. Herein, we ponder how one might strike a useful balance between these two extremes. We focus in particular on designing proteins with novel property values, although much of our discussion addresses machine learning-based design more broadly.

Prediction-Powered Inference

We introduce prediction-powered inference $\unicode{x2013}$ a framework for performing valid statistical inference when an experimental data set is supplemented with predictions from a machine-learning system. Our framework yields provably valid conclusions without making any assumptions on the machine-learning algorithm that supplies the predictions. Higher accuracy of the predictions translates to smaller confidence intervals, permitting more powerful inference. Prediction-powered inference yields simple algorithms for computing valid confidence intervals for statistical objects such as means, quantiles, and linear and logistic regression coefficients. We demonstrate the benefits of prediction-powered inference with data sets from proteomics, genomics, electronic voting, remote sensing, census analysis, and ecology.

Conformal prediction for the design problem

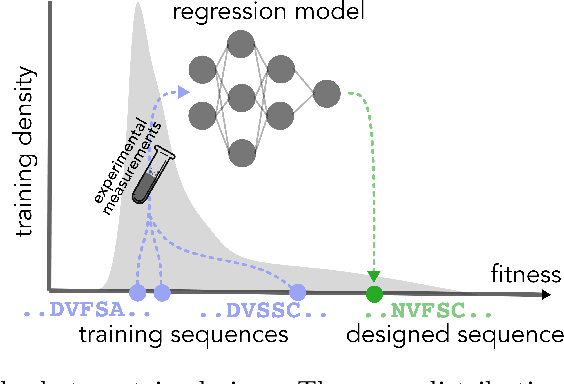
In many real-world deployments of machine learning, we use a prediction algorithm to choose what data to test next. For example, in the protein design problem, we have a regression model that predicts some real-valued property of a protein sequence, which we use to propose new sequences believed to exhibit higher property values than observed in the training data. Since validating designed sequences in the wet lab is typically costly, it is important to know how much we can trust the model's predictions. In such settings, however, there is a distinct type of distribution shift between the training and test data: one where the training and test data are statistically dependent, as the latter is chosen based on the former. Consequently, the model's error on the test data -- that is, the designed sequences -- has some non-trivial relationship with its error on the training data. Herein, we introduce a method to quantify predictive uncertainty in such settings. We do so by constructing confidence sets for predictions that account for the dependence between the training and test data. The confidence sets we construct have finite-sample guarantees that hold for any prediction algorithm, even when a trained model chooses the test-time input distribution. As a motivating use case, we demonstrate how our method quantifies uncertainty for the predicted fitness of designed protein using several real data sets.

Variational Refinement for Importance Sampling Using the Forward Kullback-Leibler Divergence

Variational Inference (VI) is a popular alternative to asymptotically exact sampling in Bayesian inference. Its main workhorse is optimization over a reverse Kullback-Leibler divergence (RKL), which typically underestimates the tail of the posterior leading to miscalibration and potential degeneracy. Importance sampling (IS), on the other hand, is often used to fine-tune and de-bias the estimates of approximate Bayesian inference procedures. The quality of IS crucially depends on the choice of the proposal distribution. Ideally, the proposal distribution has heavier tails than the target, which is rarely achievable by minimizing the RKL. We thus propose a novel combination of optimization and sampling techniques for approximate Bayesian inference by constructing an IS proposal distribution through the minimization of a forward KL (FKL) divergence. This approach guarantees asymptotic consistency and a fast convergence towards both the optimal IS estimator and the optimal variational approximation. We empirically demonstrate on real data that our method is competitive with variational boosting and MCMC.

Autofocused oracles for model-based design

Data-driven design is making headway into a number of application areas, including protein, small-molecule, and materials engineering. The design goal is to construct an object with desired properties, such as a protein that binds to a target more tightly than previously observed. To that end, costly experimental measurements are being replaced with calls to a high-capacity regression model trained on labeled data, which can be leveraged in an in silico search for promising design candidates. However, the design goal necessitates moving into regions of the input space beyond where such models were trained. Therefore, one can ask: should the regression model be altered as the design algorithm explores the input space, in the absence of new data acquisition? Herein, we answer this question in the affirmative. In particular, we (i) formalize the data-driven design problem as a non-zero-sum game, (ii) leverage this formalism to develop a strategy for retraining the regression model as the design algorithm proceeds---what we refer to as autofocusing the model, and (iii) demonstrate the promise of autofocusing empirically.

A view of Estimation of Distribution Algorithms through the lens of Expectation-Maximization

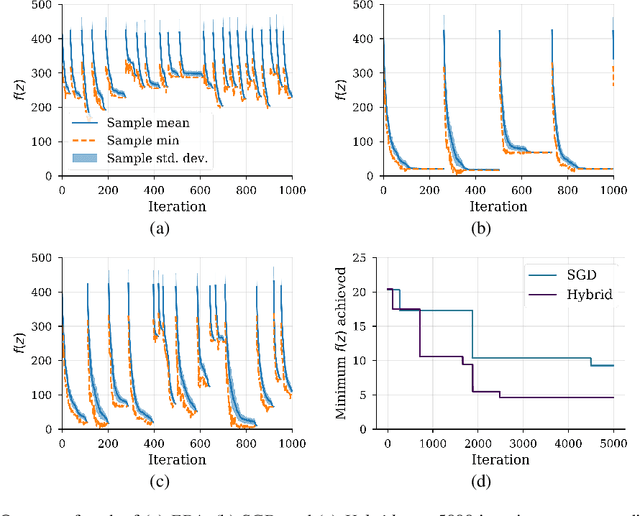
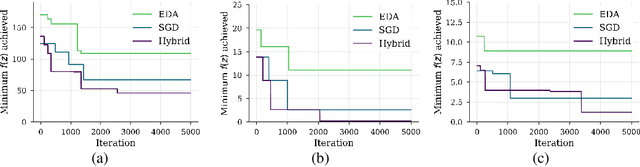
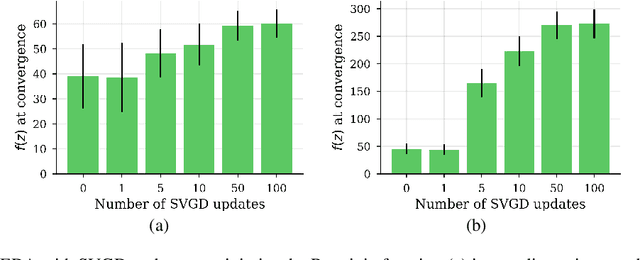
We show that under mild conditions, Estimation of Distribution Algorithms (EDAs) can be written as variational Expectation-Maximization (EM) that uses a mixture of weighted particles as the approximate posterior. In the infinite particle limit, EDAs can be viewed as exact EM. Because EM sits on a rigorous statistical foundation and has been thoroughly analyzed, this connection provides a coherent framework with which to reason about EDAs. Importantly, the connection also suggests avenues for possible improvements to EDAs owing to our ability to leverage general statistical tools and generalizations of EM. For example, we make use of results about known EM convergence properties to propose an adaptive, hybrid EDA-gradient descent algorithm; this hybrid demonstrates better performance than either component of the hybrid on several canonical, non-convex test functions. We also demonstrate empirically that although one might hypothesize that reducing the variational gap could prove useful, it actually degrades performance of EDAs. Finally, we show that the connection between EM and EDAs provides us with a new perspective on why EDAs are performing approximate natural gradient descent.