Unlocking Guidance for Discrete State-Space Diffusion and Flow Models

Generative models on discrete state-spaces have a wide range of potential applications, particularly in the domain of natural sciences. In continuous state-spaces, controllable and flexible generation of samples with desired properties has been realized using guidance on diffusion and flow models. However, these guidance approaches are not readily amenable to discrete state-space models. Consequently, we introduce a general and principled method for applying guidance on such models. Our method depends on leveraging continuous-time Markov processes on discrete state-spaces, which unlocks computational tractability for sampling from a desired guided distribution. We demonstrate the utility of our approach, Discrete Guidance, on a range of applications including guided generation of images, small-molecules, DNA sequences and protein sequences.

The perpetual motion machine of AI-generated data and the distraction of ChatGPT-as-scientist

Since ChatGPT works so well, are we on the cusp of solving science with AI? Is not AlphaFold2 suggestive that the potential of LLMs in biology and the sciences more broadly is limitless? Can we use AI itself to bridge the lack of data in the sciences in order to then train an AI? Herein we present a discussion of these topics.

Is novelty predictable?

Machine learning-based design has gained traction in the sciences, most notably in the design of small molecules, materials, and proteins, with societal implications spanning drug development and manufacturing, plastic degradation, and carbon sequestration. When designing objects to achieve novel property values with machine learning, one faces a fundamental challenge: how to push past the frontier of current knowledge, distilled from the training data into the model, in a manner that rationally controls the risk of failure. If one trusts learned models too much in extrapolation, one is likely to design rubbish. In contrast, if one does not extrapolate, one cannot find novelty. Herein, we ponder how one might strike a useful balance between these two extremes. We focus in particular on designing proteins with novel property values, although much of our discussion addresses machine learning-based design more broadly.

Augmenting Neural Networks with Priors on Function Values

The need for function estimation in label-limited settings is common in the natural sciences. At the same time, prior knowledge of function values is often available in these domains. For example, data-free biophysics-based models can be informative on protein properties, while quantum-based computations can be informative on small molecule properties. How can we coherently leverage such prior knowledge to help improve a neural network model that is quite accurate in some regions of input space -- typically near the training data -- but wildly wrong in other regions? Bayesian neural networks (BNN) enable the user to specify prior information only on the neural network weights, not directly on the function values. Moreover, there is in general no clear mapping between these. Herein, we tackle this problem by developing an approach to augment BNNs with prior information on the function values themselves. Our probabilistic approach yields predictions that rely more heavily on the prior information when the epistemic uncertainty is large, and more heavily on the neural network when the epistemic uncertainty is small.

Conformal prediction for the design problem

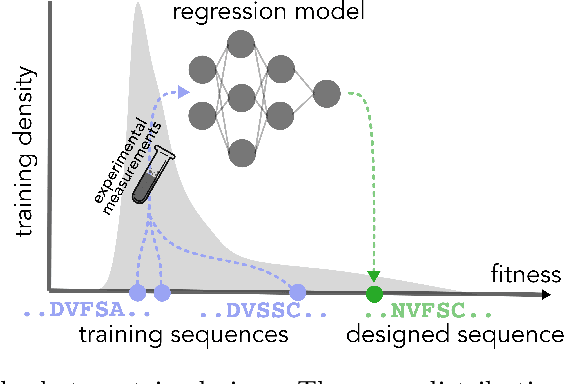
In many real-world deployments of machine learning, we use a prediction algorithm to choose what data to test next. For example, in the protein design problem, we have a regression model that predicts some real-valued property of a protein sequence, which we use to propose new sequences believed to exhibit higher property values than observed in the training data. Since validating designed sequences in the wet lab is typically costly, it is important to know how much we can trust the model's predictions. In such settings, however, there is a distinct type of distribution shift between the training and test data: one where the training and test data are statistically dependent, as the latter is chosen based on the former. Consequently, the model's error on the test data -- that is, the designed sequences -- has some non-trivial relationship with its error on the training data. Herein, we introduce a method to quantify predictive uncertainty in such settings. We do so by constructing confidence sets for predictions that account for the dependence between the training and test data. The confidence sets we construct have finite-sample guarantees that hold for any prediction algorithm, even when a trained model chooses the test-time input distribution. As a motivating use case, we demonstrate how our method quantifies uncertainty for the predicted fitness of designed protein using several real data sets.

Autofocused oracles for model-based design

Data-driven design is making headway into a number of application areas, including protein, small-molecule, and materials engineering. The design goal is to construct an object with desired properties, such as a protein that binds to a target more tightly than previously observed. To that end, costly experimental measurements are being replaced with calls to a high-capacity regression model trained on labeled data, which can be leveraged in an in silico search for promising design candidates. However, the design goal necessitates moving into regions of the input space beyond where such models were trained. Therefore, one can ask: should the regression model be altered as the design algorithm explores the input space, in the absence of new data acquisition? Herein, we answer this question in the affirmative. In particular, we (i) formalize the data-driven design problem as a non-zero-sum game, (ii) leverage this formalism to develop a strategy for retraining the regression model as the design algorithm proceeds---what we refer to as autofocusing the model, and (iii) demonstrate the promise of autofocusing empirically.

A view of Estimation of Distribution Algorithms through the lens of Expectation-Maximization

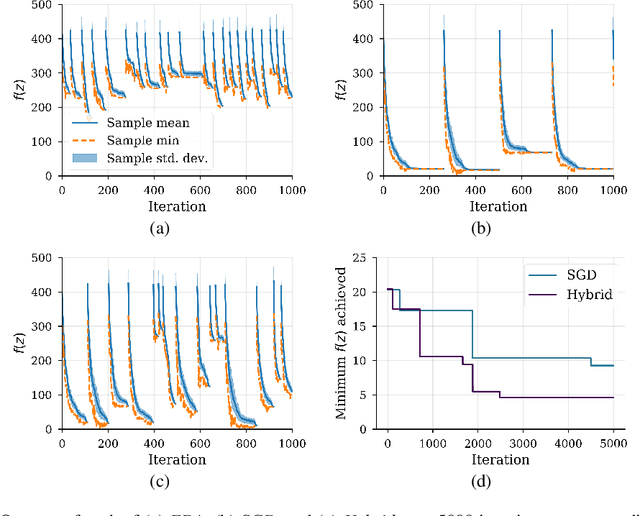
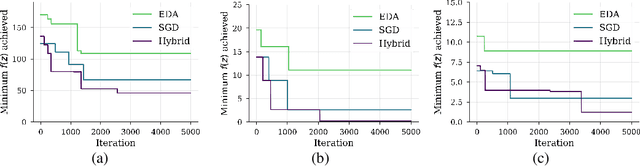
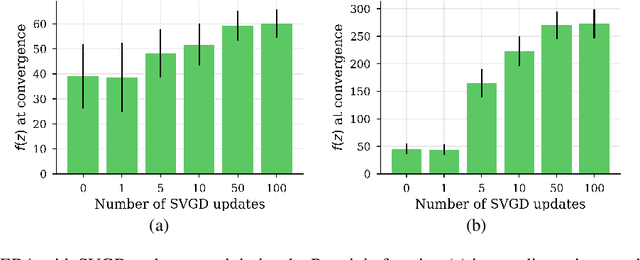
We show that under mild conditions, Estimation of Distribution Algorithms (EDAs) can be written as variational Expectation-Maximization (EM) that uses a mixture of weighted particles as the approximate posterior. In the infinite particle limit, EDAs can be viewed as exact EM. Because EM sits on a rigorous statistical foundation and has been thoroughly analyzed, this connection provides a coherent framework with which to reason about EDAs. Importantly, the connection also suggests avenues for possible improvements to EDAs owing to our ability to leverage general statistical tools and generalizations of EM. For example, we make use of results about known EM convergence properties to propose an adaptive, hybrid EDA-gradient descent algorithm; this hybrid demonstrates better performance than either component of the hybrid on several canonical, non-convex test functions. We also demonstrate empirically that although one might hypothesize that reducing the variational gap could prove useful, it actually degrades performance of EDAs. Finally, we show that the connection between EM and EDAs provides us with a new perspective on why EDAs are performing approximate natural gradient descent.

Conditioning by adaptive sampling for robust design

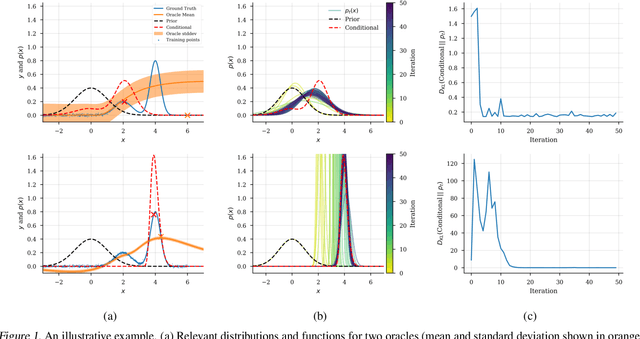
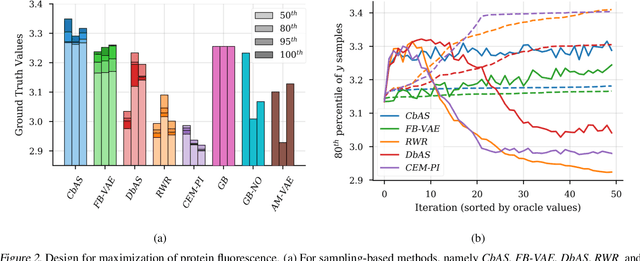
We present a new method for design problems wherein the goal is to maximize or specify the value of one or more properties of interest. For example, in protein design, one may wish to find the protein sequence that maximizes fluorescence. We assume access to one or more, potentially black box, stochastic "oracle" predictive functions, each of which maps from input (e.g., protein sequences) design space to a distribution over a property of interest (e.g. protein fluorescence). At first glance, this problem can be framed as one of optimizing the oracle(s) with respect to the input. However, many state-of-the-art predictive models, such as neural networks, are known to suffer from pathologies, especially for data far from the training distribution. Thus we need to modulate the optimization of the oracle inputs with prior knowledge about what makes `realistic' inputs (e.g., proteins that stably fold). Herein, we propose a new method to solve this problem, Conditioning by Adaptive Sampling, which yields state-of-the-art results on a protein fluorescence problem, as compared to other recently published approaches. Formally, our method achieves its success by using model-based adaptive sampling to estimate the conditional distribution of the input sequences given the desired properties.

Design by adaptive sampling

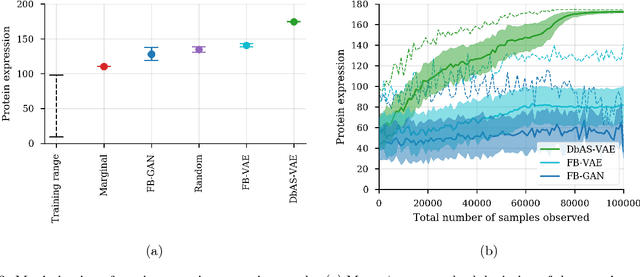
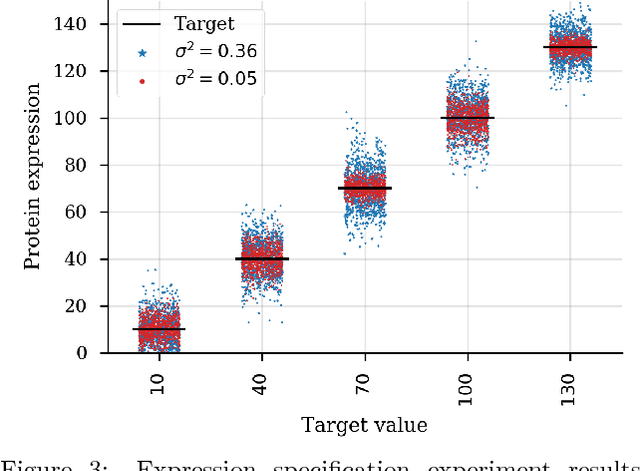
We present a probabilistic modeling framework and adaptive sampling algorithm wherein unsupervised generative models are combined with black box predictive models to tackle the problem of input design. In input design, one is given one or more stochastic "oracle" predictive functions, each of which maps from the input design space (e.g. DNA sequences or images) to a distribution over a property of interest (e.g. protein fluorescence or image content). Given such stochastic oracles, the problem is to find an input that is expected to maximize one or more properties, or to achieve a specified value of one or more properties, or any combination thereof. We demonstrate experimentally that our approach substantially outperforms other recently presented methods for tackling a specific version of this problem, namely, maximization when the oracle is assumed to be deterministic and unbiased. We also demonstrate that our method can tackle more general versions of the problem.

Gaussian Process Prior Variational Autoencoders

Variational autoencoders (VAE) are a powerful and widely-used class of models to learn complex data distributions in an unsupervised fashion. One important limitation of VAEs is the prior assumption that latent sample representations are independent and identically distributed. However, for many important datasets, such as time-series of images, this assumption is too strong: accounting for covariances between samples, such as those in time, can yield to a more appropriate model specification and improve performance in downstream tasks. In this work, we introduce a new model, the Gaussian Process (GP) Prior Variational Autoencoder (GPPVAE), to specifically address this issue. The GPPVAE aims to combine the power of VAEs with the ability to model correlations afforded by GP priors. To achieve efficient inference in this new class of models, we leverage structure in the covariance matrix, and introduce a new stochastic backpropagation strategy that allows for computing stochastic gradients in a distributed and low-memory fashion. We show that our method outperforms conditional VAEs (CVAEs) and an adaptation of standard VAEs in two image data applications.