A view of Estimation of Distribution Algorithms through the lens of Expectation-Maximization

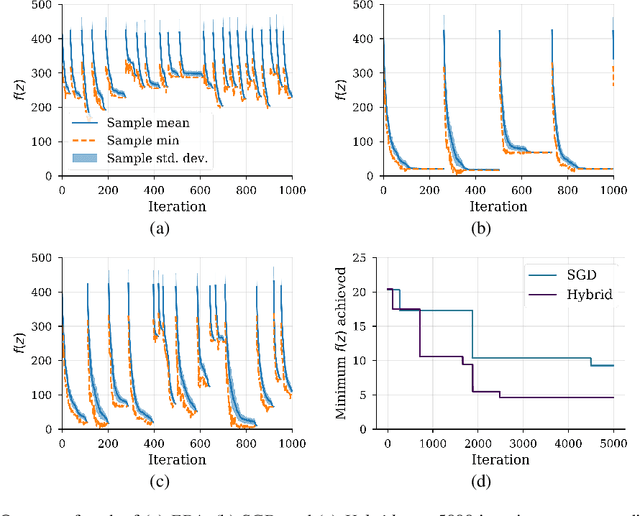
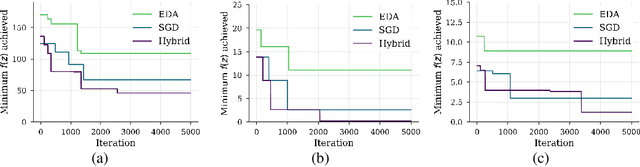
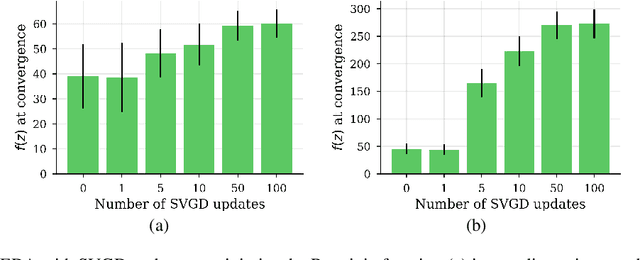
We show that under mild conditions, Estimation of Distribution Algorithms (EDAs) can be written as variational Expectation-Maximization (EM) that uses a mixture of weighted particles as the approximate posterior. In the infinite particle limit, EDAs can be viewed as exact EM. Because EM sits on a rigorous statistical foundation and has been thoroughly analyzed, this connection provides a coherent framework with which to reason about EDAs. Importantly, the connection also suggests avenues for possible improvements to EDAs owing to our ability to leverage general statistical tools and generalizations of EM. For example, we make use of results about known EM convergence properties to propose an adaptive, hybrid EDA-gradient descent algorithm; this hybrid demonstrates better performance than either component of the hybrid on several canonical, non-convex test functions. We also demonstrate empirically that although one might hypothesize that reducing the variational gap could prove useful, it actually degrades performance of EDAs. Finally, we show that the connection between EM and EDAs provides us with a new perspective on why EDAs are performing approximate natural gradient descent.