Contrastive losses as generalized models of global epistasis

Fitness functions map large combinatorial spaces of biological sequences to properties of interest. Inferring these multimodal functions from experimental data is a central task in modern protein engineering. Global epistasis models are an effective and physically-grounded class of models for estimating fitness functions from observed data. These models assume that a sparse latent function is transformed by a monotonic nonlinearity to emit measurable fitness. Here we demonstrate that minimizing contrastive loss functions, such as the Bradley-Terry loss, is a simple and flexible technique for extracting the sparse latent function implied by global epistasis. We argue by way of a fitness-epistasis uncertainty principle that the nonlinearities in global epistasis models can produce observed fitness functions that do not admit sparse representations, and thus may be inefficient to learn from observations when using a Mean Squared Error (MSE) loss (a common practice). We show that contrastive losses are able to accurately estimate a ranking function from limited data even in regimes where MSE is ineffective. We validate the practical utility of this insight by showing contrastive loss functions result in consistently improved performance on benchmark tasks.

A view of Estimation of Distribution Algorithms through the lens of Expectation-Maximization

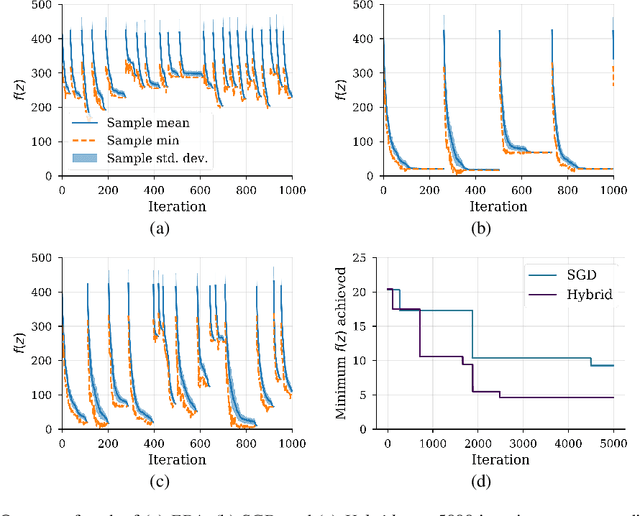
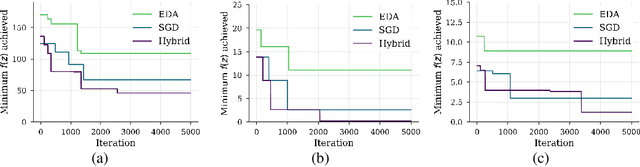
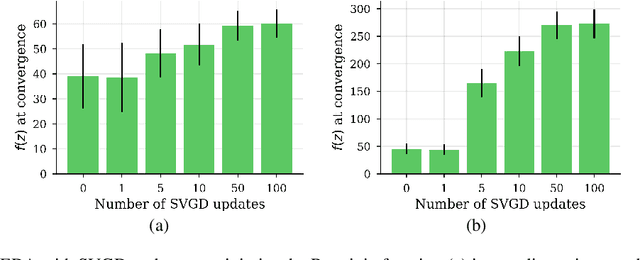
We show that under mild conditions, Estimation of Distribution Algorithms (EDAs) can be written as variational Expectation-Maximization (EM) that uses a mixture of weighted particles as the approximate posterior. In the infinite particle limit, EDAs can be viewed as exact EM. Because EM sits on a rigorous statistical foundation and has been thoroughly analyzed, this connection provides a coherent framework with which to reason about EDAs. Importantly, the connection also suggests avenues for possible improvements to EDAs owing to our ability to leverage general statistical tools and generalizations of EM. For example, we make use of results about known EM convergence properties to propose an adaptive, hybrid EDA-gradient descent algorithm; this hybrid demonstrates better performance than either component of the hybrid on several canonical, non-convex test functions. We also demonstrate empirically that although one might hypothesize that reducing the variational gap could prove useful, it actually degrades performance of EDAs. Finally, we show that the connection between EM and EDAs provides us with a new perspective on why EDAs are performing approximate natural gradient descent.

Conditioning by adaptive sampling for robust design

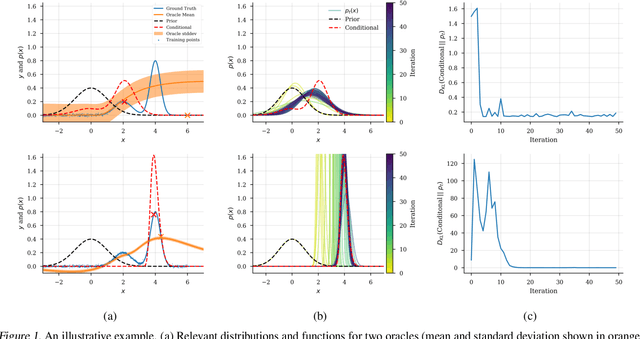
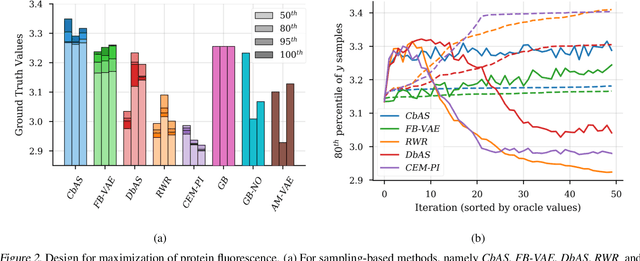
We present a new method for design problems wherein the goal is to maximize or specify the value of one or more properties of interest. For example, in protein design, one may wish to find the protein sequence that maximizes fluorescence. We assume access to one or more, potentially black box, stochastic "oracle" predictive functions, each of which maps from input (e.g., protein sequences) design space to a distribution over a property of interest (e.g. protein fluorescence). At first glance, this problem can be framed as one of optimizing the oracle(s) with respect to the input. However, many state-of-the-art predictive models, such as neural networks, are known to suffer from pathologies, especially for data far from the training distribution. Thus we need to modulate the optimization of the oracle inputs with prior knowledge about what makes `realistic' inputs (e.g., proteins that stably fold). Herein, we propose a new method to solve this problem, Conditioning by Adaptive Sampling, which yields state-of-the-art results on a protein fluorescence problem, as compared to other recently published approaches. Formally, our method achieves its success by using model-based adaptive sampling to estimate the conditional distribution of the input sequences given the desired properties.

Design by adaptive sampling

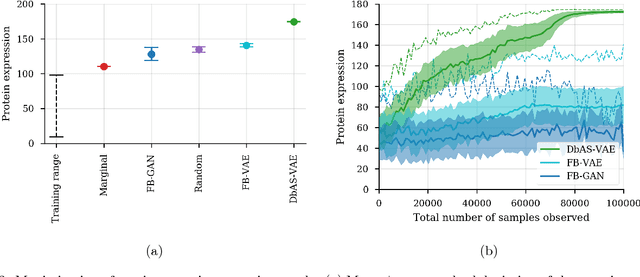
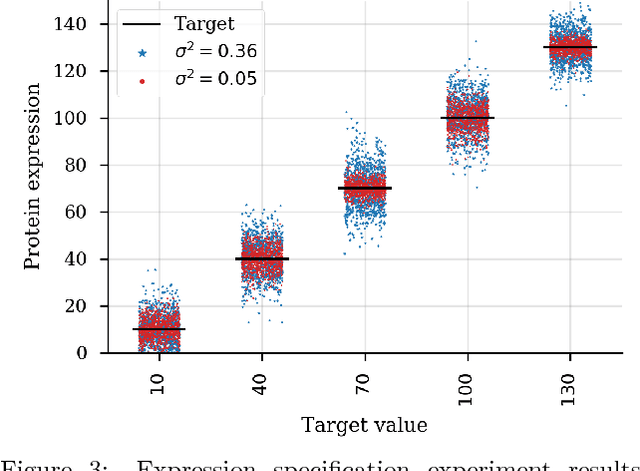
We present a probabilistic modeling framework and adaptive sampling algorithm wherein unsupervised generative models are combined with black box predictive models to tackle the problem of input design. In input design, one is given one or more stochastic "oracle" predictive functions, each of which maps from the input design space (e.g. DNA sequences or images) to a distribution over a property of interest (e.g. protein fluorescence or image content). Given such stochastic oracles, the problem is to find an input that is expected to maximize one or more properties, or to achieve a specified value of one or more properties, or any combination thereof. We demonstrate experimentally that our approach substantially outperforms other recently presented methods for tackling a specific version of this problem, namely, maximization when the oracle is assumed to be deterministic and unbiased. We also demonstrate that our method can tackle more general versions of the problem.