Conditioning by adaptive sampling for robust design
Paper and Code
Feb 06, 2019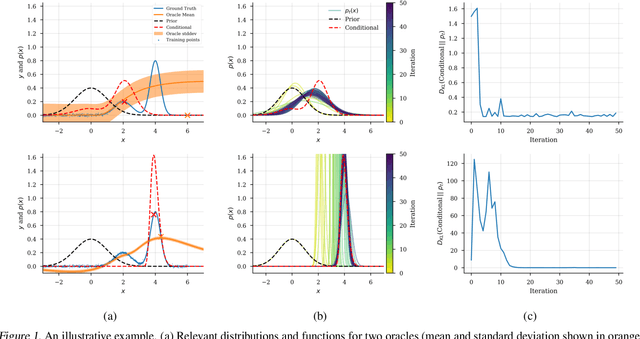
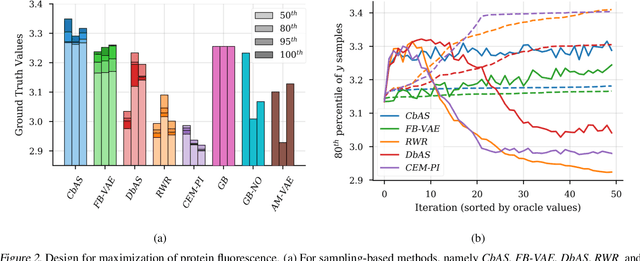
We present a new method for design problems wherein the goal is to maximize or specify the value of one or more properties of interest. For example, in protein design, one may wish to find the protein sequence that maximizes fluorescence. We assume access to one or more, potentially black box, stochastic "oracle" predictive functions, each of which maps from input (e.g., protein sequences) design space to a distribution over a property of interest (e.g. protein fluorescence). At first glance, this problem can be framed as one of optimizing the oracle(s) with respect to the input. However, many state-of-the-art predictive models, such as neural networks, are known to suffer from pathologies, especially for data far from the training distribution. Thus we need to modulate the optimization of the oracle inputs with prior knowledge about what makes `realistic' inputs (e.g., proteins that stably fold). Herein, we propose a new method to solve this problem, Conditioning by Adaptive Sampling, which yields state-of-the-art results on a protein fluorescence problem, as compared to other recently published approaches. Formally, our method achieves its success by using model-based adaptive sampling to estimate the conditional distribution of the input sequences given the desired properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge