BIOMEDICA: An Open Biomedical Image-Caption Archive, Dataset, and Vision-Language Models Derived from Scientific Literature

The development of vision-language models (VLMs) is driven by large-scale and diverse multimodal datasets. However, progress toward generalist biomedical VLMs is limited by the lack of annotated, publicly accessible datasets across biology and medicine. Existing efforts are restricted to narrow domains, missing the full diversity of biomedical knowledge encoded in scientific literature. To address this gap, we introduce BIOMEDICA, a scalable, open-source framework to extract, annotate, and serialize the entirety of the PubMed Central Open Access subset into an easy-to-use, publicly accessible dataset. Our framework produces a comprehensive archive with over 24 million unique image-text pairs from over 6 million articles. Metadata and expert-guided annotations are also provided. We demonstrate the utility and accessibility of our resource by releasing BMCA-CLIP, a suite of CLIP-style models continuously pre-trained on the BIOMEDICA dataset via streaming, eliminating the need to download 27 TB of data locally. On average, our models achieve state-of-the-art performance across 40 tasks - spanning pathology, radiology, ophthalmology, dermatology, surgery, molecular biology, parasitology, and cell biology - excelling in zero-shot classification with a 6.56% average improvement (as high as 29.8% and 17.5% in dermatology and ophthalmology, respectively), and stronger image-text retrieval, all while using 10x less compute. To foster reproducibility and collaboration, we release our codebase and dataset for the broader research community.

Generalizable Neural Fields as Partially Observed Neural Processes

Neural fields, which represent signals as a function parameterized by a neural network, are a promising alternative to traditional discrete vector or grid-based representations. Compared to discrete representations, neural representations both scale well with increasing resolution, are continuous, and can be many-times differentiable. However, given a dataset of signals that we would like to represent, having to optimize a separate neural field for each signal is inefficient, and cannot capitalize on shared information or structures among signals. Existing generalization methods view this as a meta-learning problem and employ gradient-based meta-learning to learn an initialization which is then fine-tuned with test-time optimization, or learn hypernetworks to produce the weights of a neural field. We instead propose a new paradigm that views the large-scale training of neural representations as a part of a partially-observed neural process framework, and leverage neural process algorithms to solve this task. We demonstrate that this approach outperforms both state-of-the-art gradient-based meta-learning approaches and hypernetwork approaches.

Hyperbolic Deep Learning in Computer Vision: A Survey

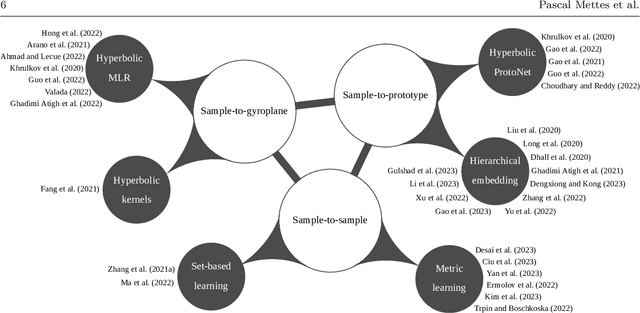
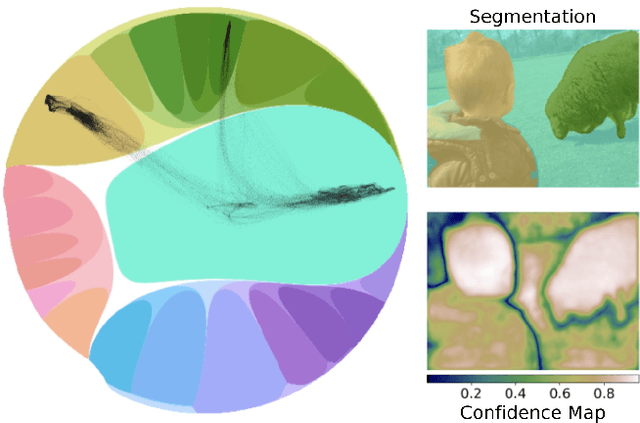
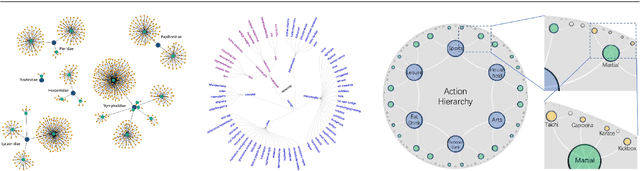
Deep representation learning is a ubiquitous part of modern computer vision. While Euclidean space has been the de facto standard manifold for learning visual representations, hyperbolic space has recently gained rapid traction for learning in computer vision. Specifically, hyperbolic learning has shown a strong potential to embed hierarchical structures, learn from limited samples, quantify uncertainty, add robustness, limit error severity, and more. In this paper, we provide a categorization and in-depth overview of current literature on hyperbolic learning for computer vision. We research both supervised and unsupervised literature and identify three main research themes in each direction. We outline how hyperbolic learning is performed in all themes and discuss the main research problems that benefit from current advances in hyperbolic learning for computer vision. Moreover, we provide a high-level intuition behind hyperbolic geometry and outline open research questions to further advance research in this direction.

NeMo: 3D Neural Motion Fields from Multiple Video Instances of the Same Action

The task of reconstructing 3D human motion has wideranging applications. The gold standard Motion capture (MoCap) systems are accurate but inaccessible to the general public due to their cost, hardware and space constraints. In contrast, monocular human mesh recovery (HMR) methods are much more accessible than MoCap as they take single-view videos as inputs. Replacing the multi-view Mo- Cap systems with a monocular HMR method would break the current barriers to collecting accurate 3D motion thus making exciting applications like motion analysis and motiondriven animation accessible to the general public. However, performance of existing HMR methods degrade when the video contains challenging and dynamic motion that is not in existing MoCap datasets used for training. This reduces its appeal as dynamic motion is frequently the target in 3D motion recovery in the aforementioned applications. Our study aims to bridge the gap between monocular HMR and multi-view MoCap systems by leveraging information shared across multiple video instances of the same action. We introduce the Neural Motion (NeMo) field. It is optimized to represent the underlying 3D motions across a set of videos of the same action. Empirically, we show that NeMo can recover 3D motion in sports using videos from the Penn Action dataset, where NeMo outperforms existing HMR methods in terms of 2D keypoint detection. To further validate NeMo using 3D metrics, we collected a small MoCap dataset mimicking actions in Penn Action,and show that NeMo achieves better 3D reconstruction compared to various baselines.

Staying in Shape: Learning Invariant Shape Representations using Contrastive Learning

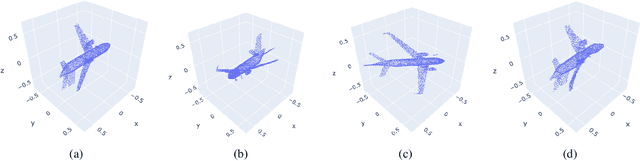
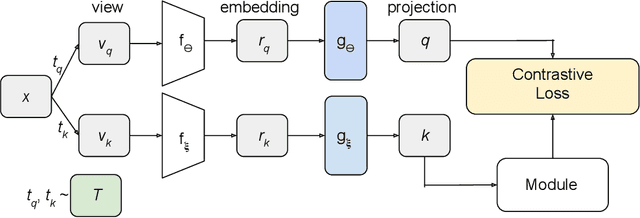
Creating representations of shapes that are invari-ant to isometric or almost-isometric transforma-tions has long been an area of interest in shape anal-ysis, since enforcing invariance allows the learningof more effective and robust shape representations.Most existing invariant shape representations arehandcrafted, and previous work on learning shaperepresentations do not focus on producing invariantrepresentations. To solve the problem of learningunsupervised invariant shape representations, weuse contrastive learning, which produces discrimi-native representations through learning invarianceto user-specified data augmentations. To producerepresentations that are specifically isometry andalmost-isometry invariant, we propose new dataaugmentations that randomly sample these transfor-mations. We show experimentally that our methodoutperforms previous unsupervised learning ap-proaches in both effectiveness and robustness.

Learning Hyperbolic Representations for Unsupervised 3D Segmentation

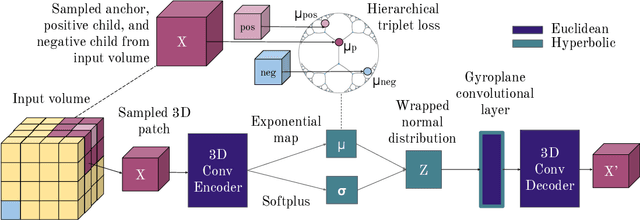
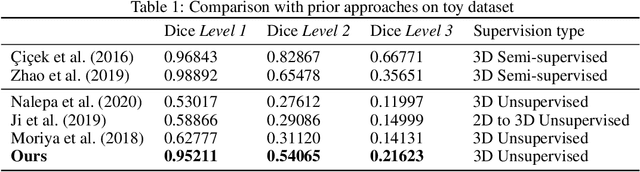
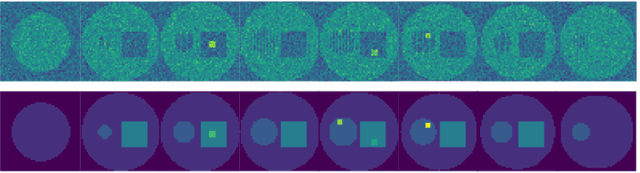
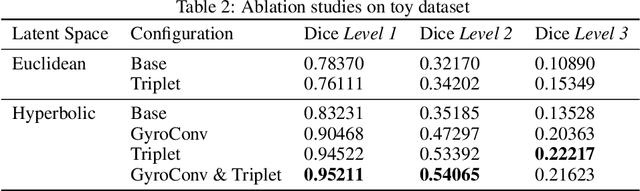
There exists a need for unsupervised 3D segmentation on complex volumetric data, particularly when annotation ability is limited or discovery of new categories is desired. Using the observation that much of 3D volumetric data is innately hierarchical, we propose learning effective representations of 3D patches for unsupervised segmentation through a variational autoencoder (VAE) with a hyperbolic latent space and a proposed gyroplane convolutional layer, which better models the underlying hierarchical structure within a 3D image. We also introduce a hierarchical triplet loss and multi-scale patch sampling scheme to embed relationships across varying levels of granularity. We demonstrate the effectiveness of our hyperbolic representations for unsupervised 3D segmentation on a hierarchical toy dataset, BraTS whole tumor dataset, and cryogenic electron microscopy data.