Emergence of heavy tails in homogenized stochastic gradient descent

It has repeatedly been observed that loss minimization by stochastic gradient descent (SGD) leads to heavy-tailed distributions of neural network parameters. Here, we analyze a continuous diffusion approximation of SGD, called homogenized stochastic gradient descent, show that it behaves asymptotically heavy-tailed, and give explicit upper and lower bounds on its tail-index. We validate these bounds in numerical experiments and show that they are typically close approximations to the empirical tail-index of SGD iterates. In addition, their explicit form enables us to quantify the interplay between optimization parameters and the tail-index. Doing so, we contribute to the ongoing discussion on links between heavy tails and the generalization performance of neural networks as well as the ability of SGD to avoid suboptimal local minima.

Hyperbolic Deep Learning in Computer Vision: A Survey

Deep representation learning is a ubiquitous part of modern computer vision. While Euclidean space has been the de facto standard manifold for learning visual representations, hyperbolic space has recently gained rapid traction for learning in computer vision. Specifically, hyperbolic learning has shown a strong potential to embed hierarchical structures, learn from limited samples, quantify uncertainty, add robustness, limit error severity, and more. In this paper, we provide a categorization and in-depth overview of current literature on hyperbolic learning for computer vision. We research both supervised and unsupervised literature and identify three main research themes in each direction. We outline how hyperbolic learning is performed in all themes and discuss the main research problems that benefit from current advances in hyperbolic learning for computer vision. Moreover, we provide a high-level intuition behind hyperbolic geometry and outline open research questions to further advance research in this direction.

Strain-Minimizing Hyperbolic Network Embeddings with Landmarks

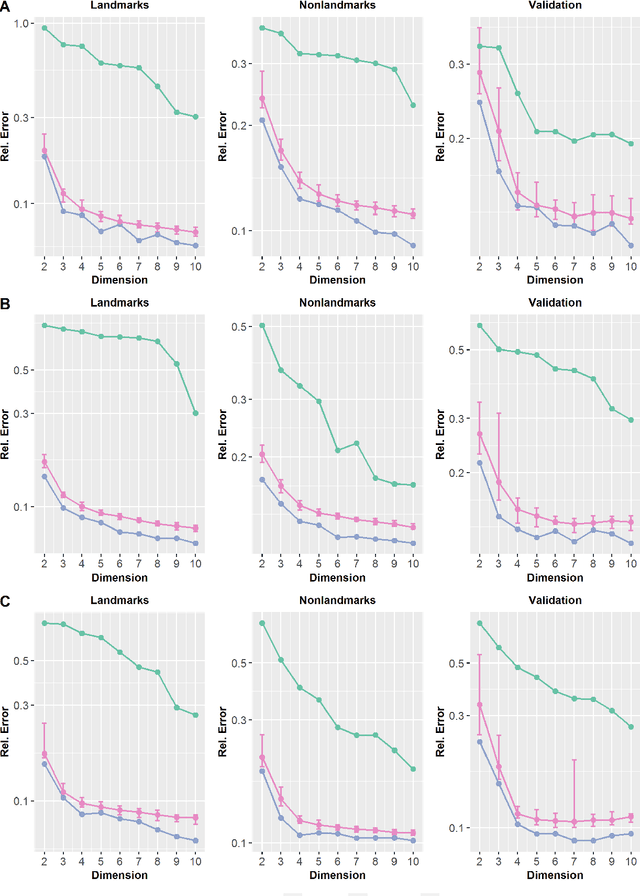
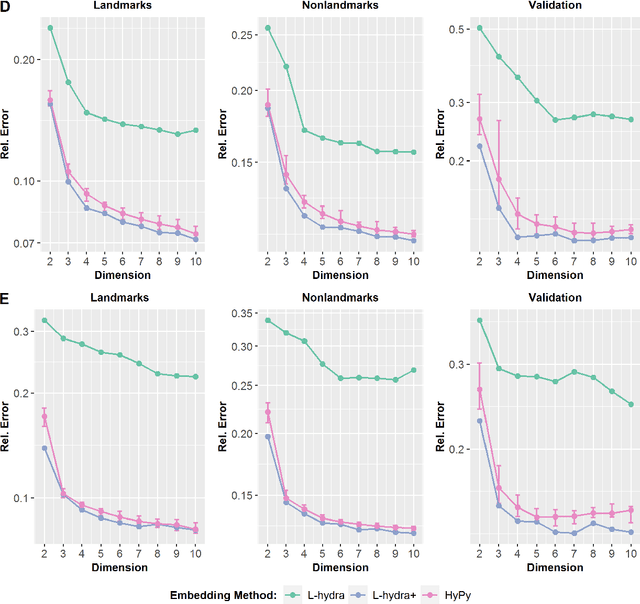
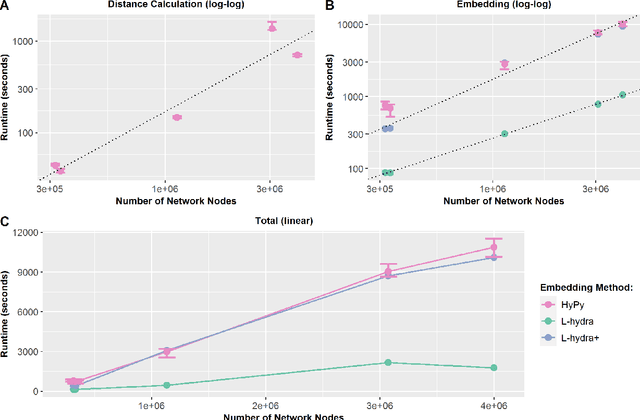
We introduce L-hydra (landmarked hyperbolic distance recovery and approximation), a method for embedding network- or distance-based data into hyperbolic space, which requires only the distance measurements to a few 'landmark nodes'. This landmark heuristic makes L-hydra applicable to large-scale graphs and improves upon previously introduced methods. As a mathematical justification, we show that a point configuration in d-dimensional hyperbolic space can be perfectly recovered (up to isometry) from distance measurements to just d+1 landmarks. We also show that L-hydra solves a two-stage strain-minimization problem, similar to our previous (unlandmarked) method 'hydra'. Testing on real network data, we show that L-hydra is an order of magnitude faster than existing hyperbolic embedding methods and scales linearly in the number of nodes. While the embedding error of L-hydra is higher than the error of existing methods, we introduce an extension, L-hydra+, which outperforms existing methods in both runtime and embedding quality.

Hyperbolic Busemann Learning with Ideal Prototypes

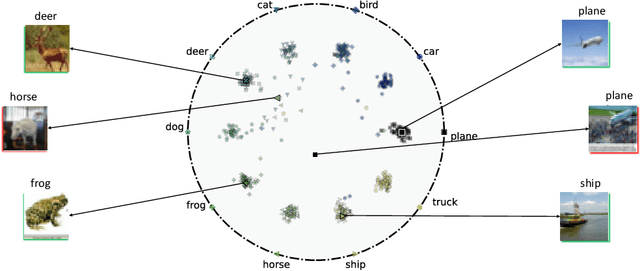
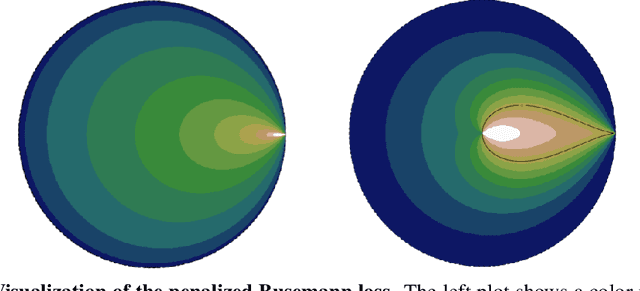
Hyperbolic space has become a popular choice of manifold for representation learning of arbitrary data, from tree-like structures and text to graphs. Building on the success of deep learning with prototypes in Euclidean and hyperspherical spaces, a few recent works have proposed hyperbolic prototypes for classification. Such approaches enable effective learning in low-dimensional output spaces and can exploit hierarchical relations amongst classes, but require privileged information about class labels to position the hyperbolic prototypes. In this work, we propose Hyperbolic Busemann Learning. The main idea behind our approach is to position prototypes on the ideal boundary of the Poincare ball, which does not require prior label knowledge. To be able to compute proximities to ideal prototypes, we introduce the penalised Busemann loss. We provide theory supporting the use of ideal prototypes and the proposed loss by proving its equivalence to logistic regression in the one-dimensional case. Empirically, we show that our approach provides a natural interpretation of classification confidence, while outperforming recent hyperspherical and hyperbolic prototype approaches.

A Theory of Hyperbolic Prototype Learning

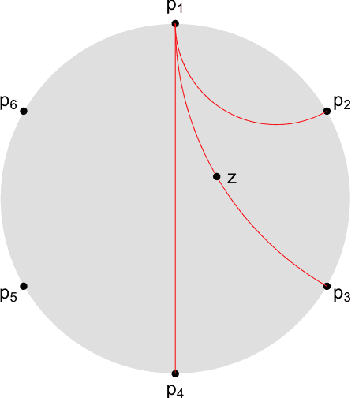
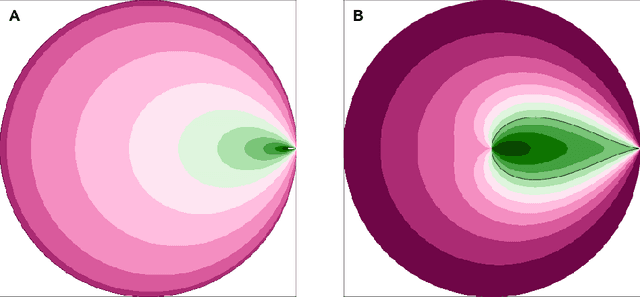
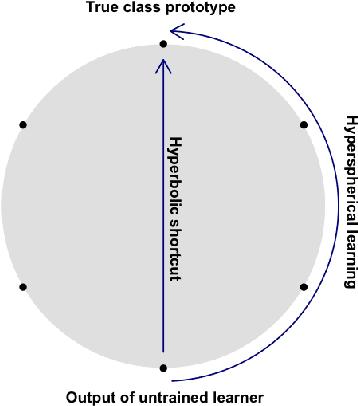
We introduce Hyperbolic Prototype Learning, a type of supervised learning, where class labels are represented by ideal points (points at infinity) in hyperbolic space. Learning is achieved by minimizing the 'penalized Busemann loss', a new loss function based on the Busemann function of hyperbolic geometry. We discuss several theoretical features of this setup. In particular, Hyperbolic Prototype Learning becomes equivalent to logistic regression in the one-dimensional case.

Hydra: A method for strain-minimizing hyperbolic embedding

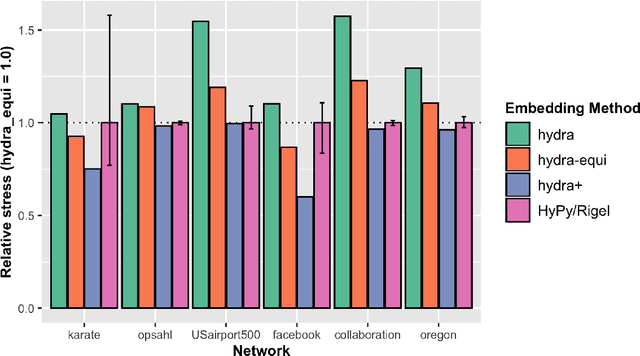
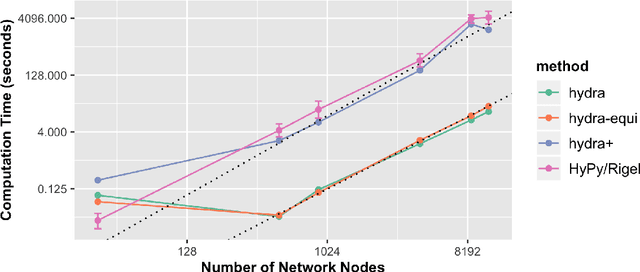
We introduce hydra (hyperbolic distance recovery and approximation), a new method for embedding network- or distance-based data into hyperbolic space. We show mathematically that hydra satisfies a certain optimality guarantee: It minimizes the 'hyperbolic strain' between original and embedded data points. Moreover, it recovers points exactly, when they are located on a hyperbolic submanifold of the feature space. Testing on real network data we show that hydra typically outperforms existing hyperbolic embedding methods in terms of embedding quality.