Strain-Minimizing Hyperbolic Network Embeddings with Landmarks

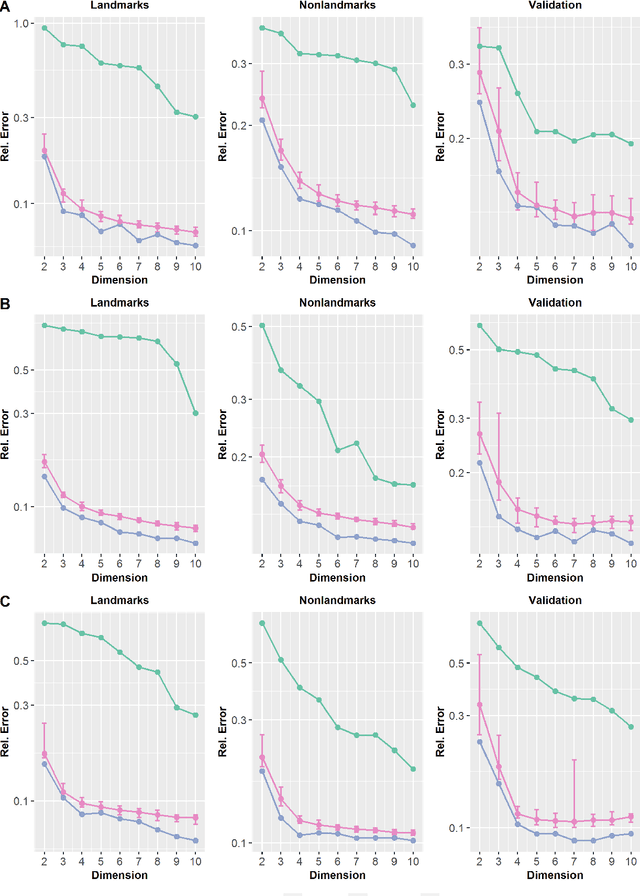
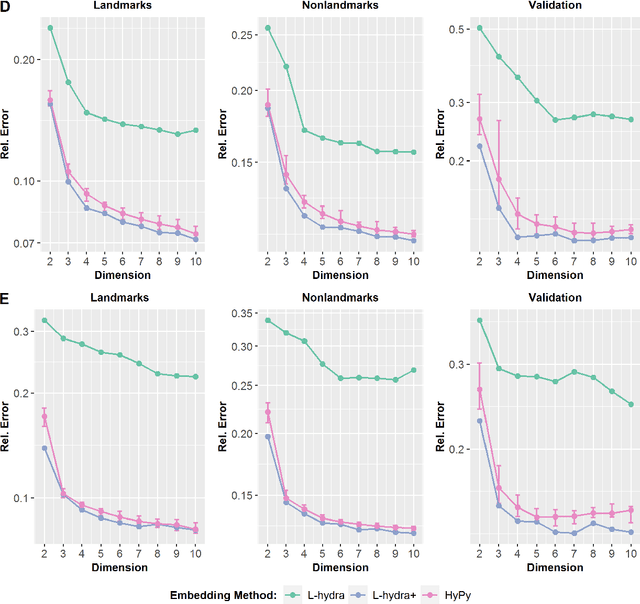
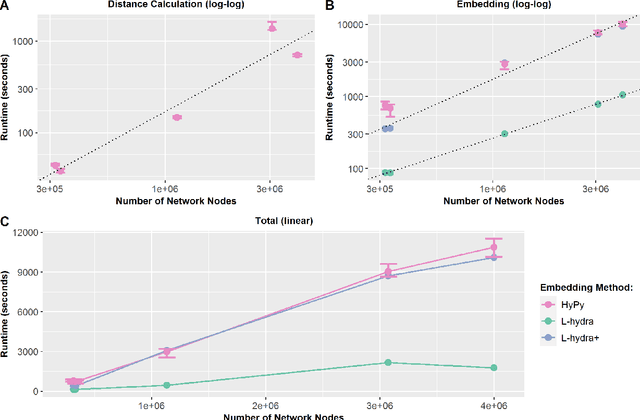
We introduce L-hydra (landmarked hyperbolic distance recovery and approximation), a method for embedding network- or distance-based data into hyperbolic space, which requires only the distance measurements to a few 'landmark nodes'. This landmark heuristic makes L-hydra applicable to large-scale graphs and improves upon previously introduced methods. As a mathematical justification, we show that a point configuration in d-dimensional hyperbolic space can be perfectly recovered (up to isometry) from distance measurements to just d+1 landmarks. We also show that L-hydra solves a two-stage strain-minimization problem, similar to our previous (unlandmarked) method 'hydra'. Testing on real network data, we show that L-hydra is an order of magnitude faster than existing hyperbolic embedding methods and scales linearly in the number of nodes. While the embedding error of L-hydra is higher than the error of existing methods, we introduce an extension, L-hydra+, which outperforms existing methods in both runtime and embedding quality.

Hydra: A method for strain-minimizing hyperbolic embedding

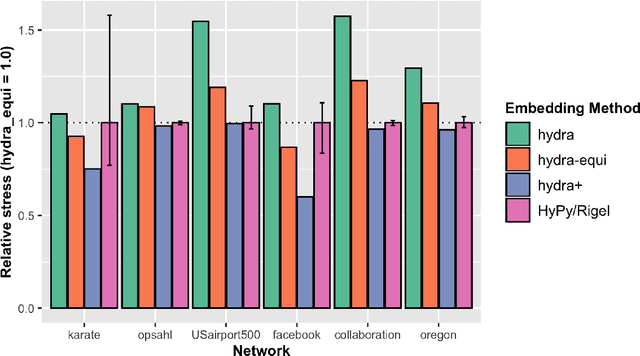
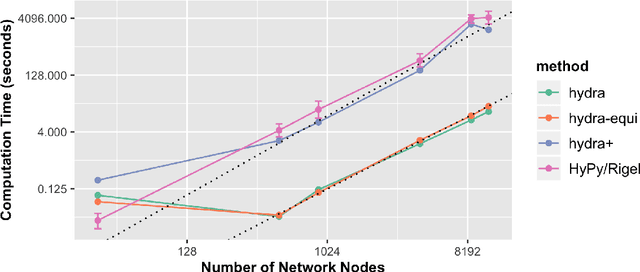
We introduce hydra (hyperbolic distance recovery and approximation), a new method for embedding network- or distance-based data into hyperbolic space. We show mathematically that hydra satisfies a certain optimality guarantee: It minimizes the 'hyperbolic strain' between original and embedded data points. Moreover, it recovers points exactly, when they are located on a hyperbolic submanifold of the feature space. Testing on real network data we show that hydra typically outperforms existing hyperbolic embedding methods in terms of embedding quality.