Hydra: A method for strain-minimizing hyperbolic embedding

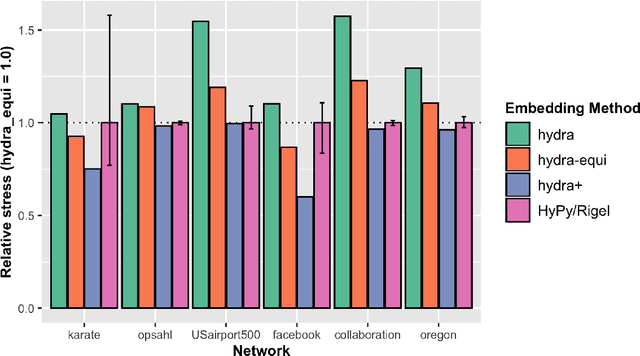
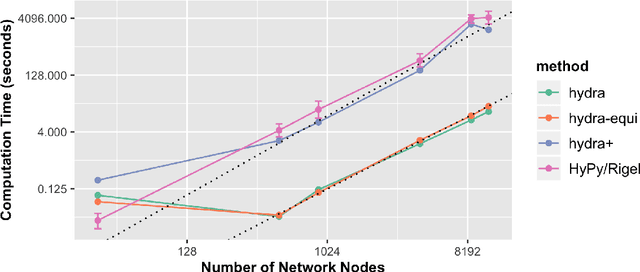
We introduce hydra (hyperbolic distance recovery and approximation), a new method for embedding network- or distance-based data into hyperbolic space. We show mathematically that hydra satisfies a certain optimality guarantee: It minimizes the 'hyperbolic strain' between original and embedded data points. Moreover, it recovers points exactly, when they are located on a hyperbolic submanifold of the feature space. Testing on real network data we show that hydra typically outperforms existing hyperbolic embedding methods in terms of embedding quality.