A Theory of Hyperbolic Prototype Learning
Paper and Code
Oct 15, 2020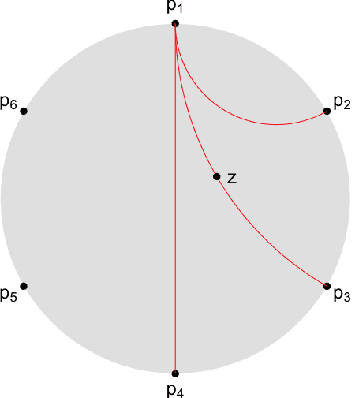
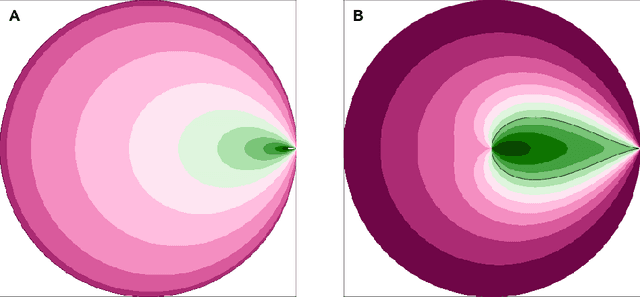
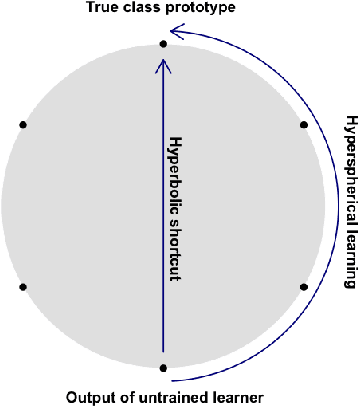
We introduce Hyperbolic Prototype Learning, a type of supervised learning, where class labels are represented by ideal points (points at infinity) in hyperbolic space. Learning is achieved by minimizing the 'penalized Busemann loss', a new loss function based on the Busemann function of hyperbolic geometry. We discuss several theoretical features of this setup. In particular, Hyperbolic Prototype Learning becomes equivalent to logistic regression in the one-dimensional case.
* 6 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge