Feature-weighted elastic net: using "features of features" for better prediction

In some supervised learning settings, the practitioner might have additional information on the features used for prediction. We propose a new method which leverages this additional information for better prediction. The method, which we call the feature-weighted elastic net ("fwelnet"), uses these "features of features" to adapt the relative penalties on the feature coefficients in the elastic net penalty. In our simulations, fwelnet outperforms the lasso in terms of test mean squared error and usually gives an improvement in true positive rate or false positive rate for feature selection. We also apply this method to early prediction of preeclampsia, where fwelnet outperforms the lasso in terms of 10-fold cross-validated area under the curve (0.86 vs. 0.80). We also provide a connection between fwelnet and the group lasso and suggest how fwelnet might be used for multi-task learning.

Reluctant generalized additive modeling

Sparse generalized additive models (GAMs) are an extension of sparse generalized linear models which allow a model's prediction to vary non-linearly with an input variable. This enables the data analyst build more accurate models, especially when the linearity assumption is known to be a poor approximation of reality. Motivated by reluctant interaction modeling (Yu et al. 2019), we propose a multi-stage algorithm, called $\textit{reluctant generalized additive modeling (RGAM)}$, that can fit sparse generalized additive models at scale. It is guided by the principle that, if all else is equal, one should prefer a linear feature over a non-linear feature. Unlike existing methods for sparse GAMs, RGAM can be extended easily to binary, count and survival data. We demonstrate the method's effectiveness on real and simulated examples.

Principal component-guided sparse regression

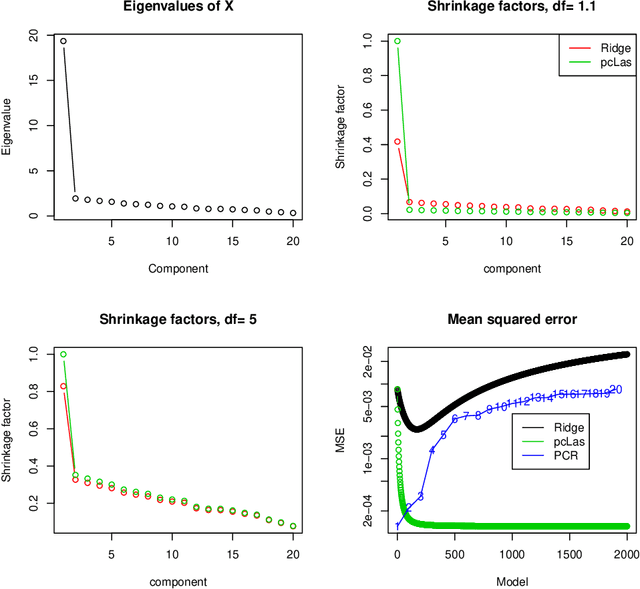
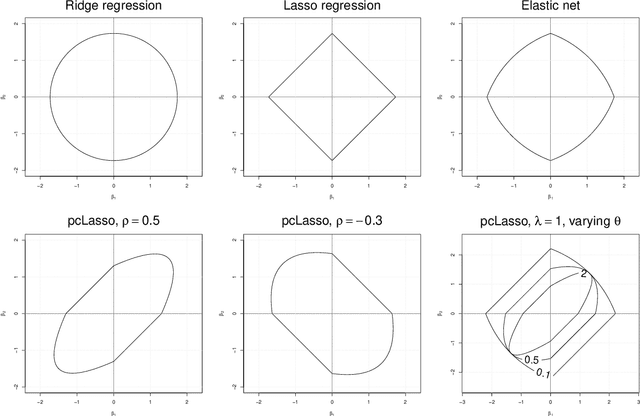
We propose a new method for supervised learning, especially suited to wide data where the number of features is much greater than the number of observations. The method combines the lasso ($\ell_1$) sparsity penalty with a quadratic penalty that shrinks the coefficient vector toward the leading principal components of the feature matrix. We call the proposed method the "principal components lasso" ("pcLasso"). The method can be especially powerful if the features are pre-assigned to groups (such as cell-pathways, assays or protein interaction networks). In that case, pcLasso shrinks each group-wise component of the solution toward the leading principal components of that group. In the process, it also carries out selection of the feature groups. We provide some theory for this method and illustrate it on a number of simulated and real data examples.