Principal component-guided sparse regression

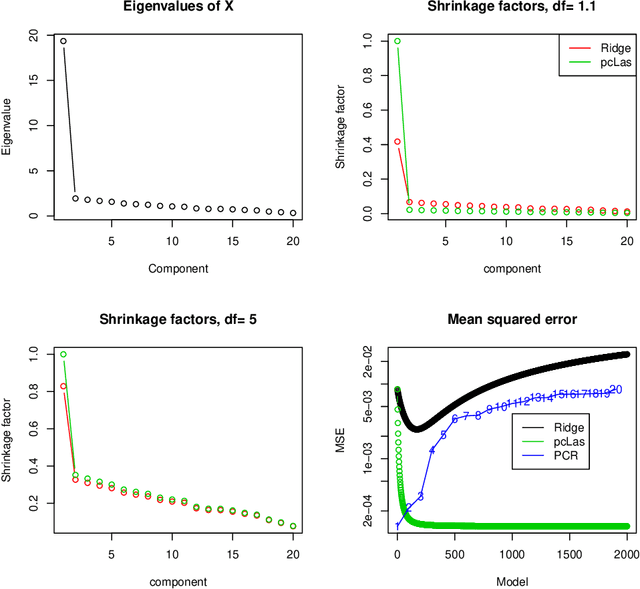
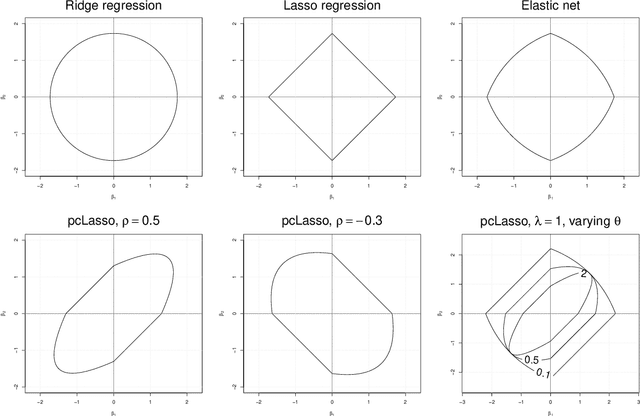
We propose a new method for supervised learning, especially suited to wide data where the number of features is much greater than the number of observations. The method combines the lasso ($\ell_1$) sparsity penalty with a quadratic penalty that shrinks the coefficient vector toward the leading principal components of the feature matrix. We call the proposed method the "principal components lasso" ("pcLasso"). The method can be especially powerful if the features are pre-assigned to groups (such as cell-pathways, assays or protein interaction networks). In that case, pcLasso shrinks each group-wise component of the solution toward the leading principal components of that group. In the process, it also carries out selection of the feature groups. We provide some theory for this method and illustrate it on a number of simulated and real data examples.

A Blockwise Descent Algorithm for Group-penalized Multiresponse and Multinomial Regression

In this paper we purpose a blockwise descent algorithm for group-penalized multiresponse regression. Using a quasi-newton framework we extend this to group-penalized multinomial regression. We give a publicly available implementation for these in R, and compare the speed of this algorithm to a competing algorithm --- we show that our implementation is an order of magnitude faster than its competitor, and can solve gene-expression-sized problems in real time.

Strong rules for discarding predictors in lasso-type problems

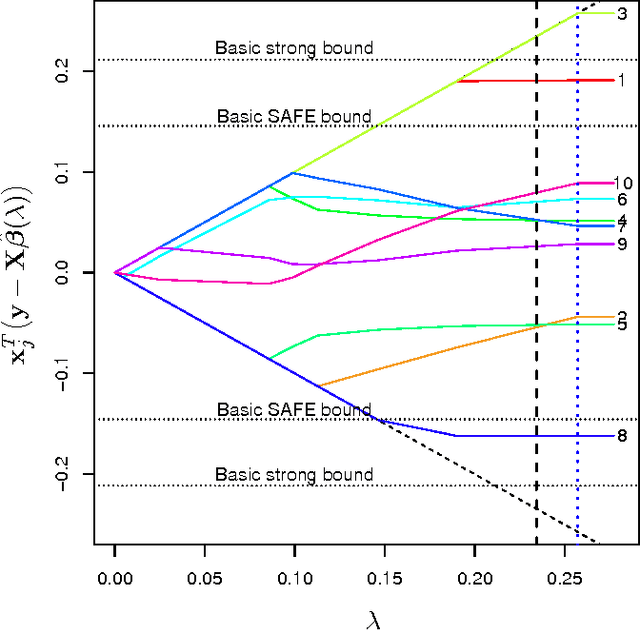
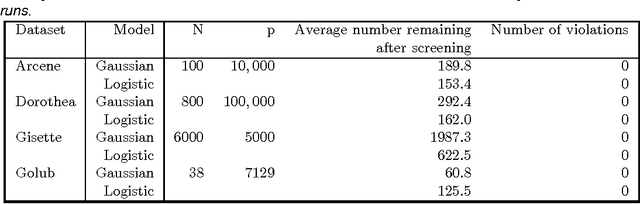
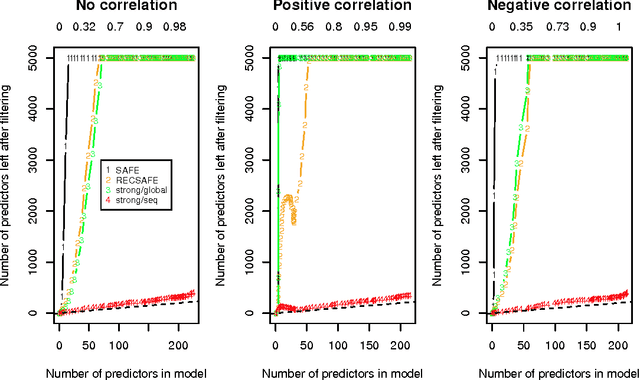
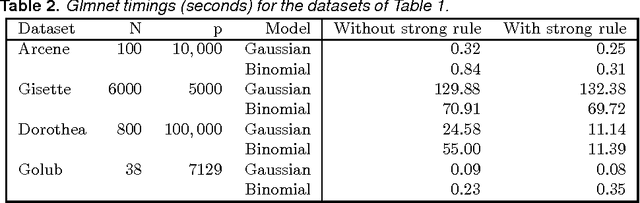
We consider rules for discarding predictors in lasso regression and related problems, for computational efficiency. El Ghaoui et al (2010) propose "SAFE" rules that guarantee that a coefficient will be zero in the solution, based on the inner products of each predictor with the outcome. In this paper we propose strong rules that are not foolproof but rarely fail in practice. These can be complemented with simple checks of the Karush- Kuhn-Tucker (KKT) conditions to provide safe rules that offer substantial speed and space savings in a variety of statistical convex optimization problems.