Strong rules for discarding predictors in lasso-type problems
Paper and Code
Nov 24, 2010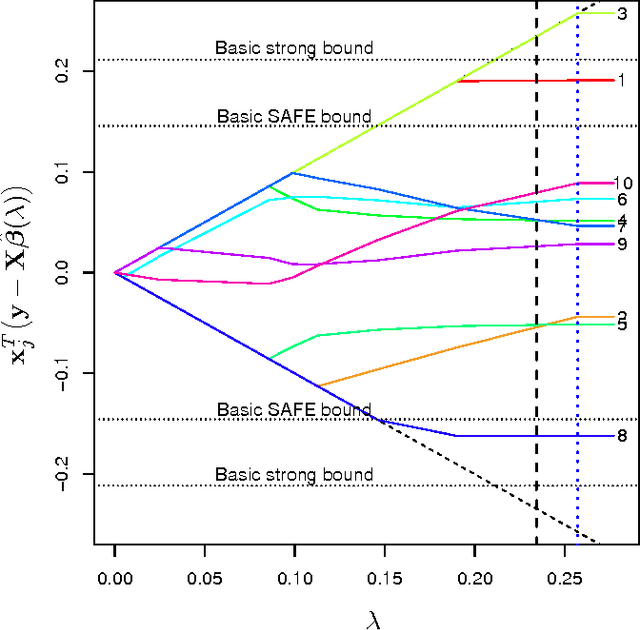
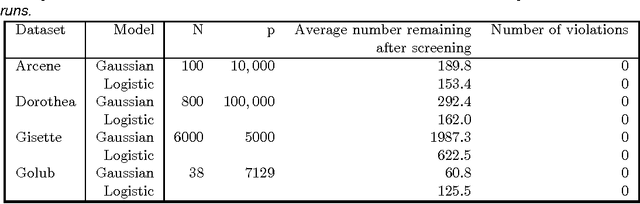
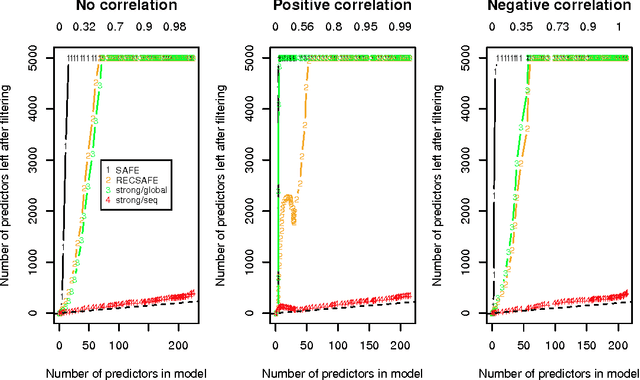
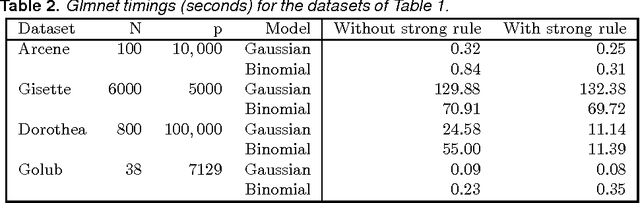
We consider rules for discarding predictors in lasso regression and related problems, for computational efficiency. El Ghaoui et al (2010) propose "SAFE" rules that guarantee that a coefficient will be zero in the solution, based on the inner products of each predictor with the outcome. In this paper we propose strong rules that are not foolproof but rarely fail in practice. These can be complemented with simple checks of the Karush- Kuhn-Tucker (KKT) conditions to provide safe rules that offer substantial speed and space savings in a variety of statistical convex optimization problems.
* 5
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge