Dimension-free Private Mean Estimation for Anisotropic Distributions

We present differentially private algorithms for high-dimensional mean estimation. Previous private estimators on distributions over $\mathbb{R}^d$ suffer from a curse of dimensionality, as they require $\Omega(d^{1/2})$ samples to achieve non-trivial error, even in cases where $O(1)$ samples suffice without privacy. This rate is unavoidable when the distribution is isotropic, namely, when the covariance is a multiple of the identity matrix, or when accuracy is measured with respect to the affine-invariant Mahalanobis distance. Yet, real-world data is often highly anisotropic, with signals concentrated on a small number of principal components. We develop estimators that are appropriate for such signals$\unicode{x2013}$our estimators are $(\varepsilon,\delta)$-differentially private and have sample complexity that is dimension-independent for anisotropic subgaussian distributions. Given $n$ samples from a distribution with known covariance-proxy $\Sigma$ and unknown mean $\mu$, we present an estimator $\hat{\mu}$ that achieves error $\|\hat{\mu}-\mu\|_2\leq \alpha$, as long as $n\gtrsim\mathrm{tr}(\Sigma)/\alpha^2+ \mathrm{tr}(\Sigma^{1/2})/(\alpha\varepsilon)$. In particular, when $\pmb{\sigma}^2=(\sigma_1^2, \ldots, \sigma_d^2)$ are the singular values of $\Sigma$, we have $\mathrm{tr}(\Sigma)=\|\pmb{\sigma}\|_2^2$ and $\mathrm{tr}(\Sigma^{1/2})=\|\pmb{\sigma}\|_1$, and hence our bound avoids dimension-dependence when the signal is concentrated in a few principal components. We show that this is the optimal sample complexity for this task up to logarithmic factors. Moreover, for the case of unknown covariance, we present an algorithm whose sample complexity has improved dependence on the dimension, from $d^{1/2}$ to $d^{1/4}$.

Fairness-Aware Meta-Learning via Nash Bargaining

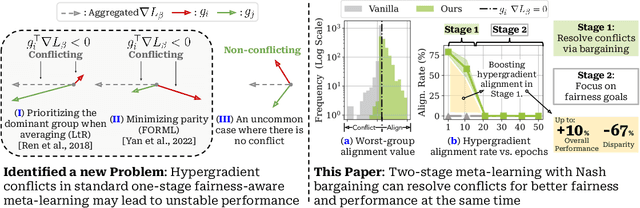
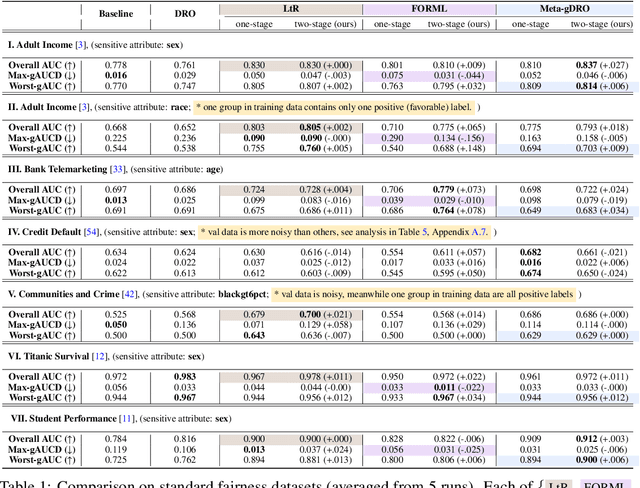
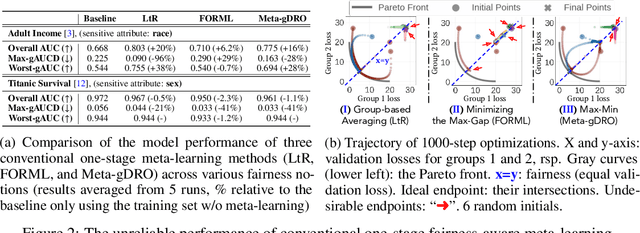
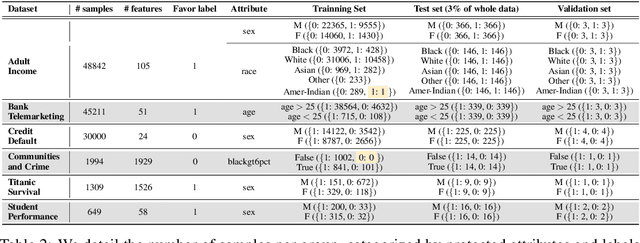
To address issues of group-level fairness in machine learning, it is natural to adjust model parameters based on specific fairness objectives over a sensitive-attributed validation set. Such an adjustment procedure can be cast within a meta-learning framework. However, naive integration of fairness goals via meta-learning can cause hypergradient conflicts for subgroups, resulting in unstable convergence and compromising model performance and fairness. To navigate this issue, we frame the resolution of hypergradient conflicts as a multi-player cooperative bargaining game. We introduce a two-stage meta-learning framework in which the first stage involves the use of a Nash Bargaining Solution (NBS) to resolve hypergradient conflicts and steer the model toward the Pareto front, and the second stage optimizes with respect to specific fairness goals. Our method is supported by theoretical results, notably a proof of the NBS for gradient aggregation free from linear independence assumptions, a proof of Pareto improvement, and a proof of monotonic improvement in validation loss. We also show empirical effects across various fairness objectives in six key fairness datasets and two image classification tasks.

CLEVRER-Humans: Describing Physical and Causal Events the Human Way

Building machines that can reason about physical events and their causal relationships is crucial for flexible interaction with the physical world. However, most existing physical and causal reasoning benchmarks are exclusively based on synthetically generated events and synthetic natural language descriptions of causal relationships. This design brings up two issues. First, there is a lack of diversity in both event types and natural language descriptions; second, causal relationships based on manually-defined heuristics are different from human judgments. To address both shortcomings, we present the CLEVRER-Humans benchmark, a video reasoning dataset for causal judgment of physical events with human labels. We employ two techniques to improve data collection efficiency: first, a novel iterative event cloze task to elicit a new representation of events in videos, which we term Causal Event Graphs (CEGs); second, a data augmentation technique based on neural language generative models. We convert the collected CEGs into questions and answers to be consistent with prior work. Finally, we study a collection of baseline approaches for CLEVRER-Humans question-answering, highlighting the great challenges set forth by our benchmark.

FastCPH: Efficient Survival Analysis for Neural Networks

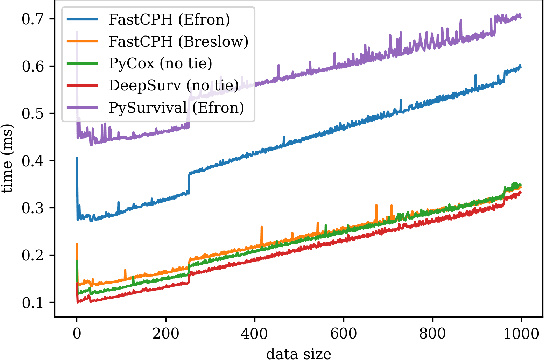
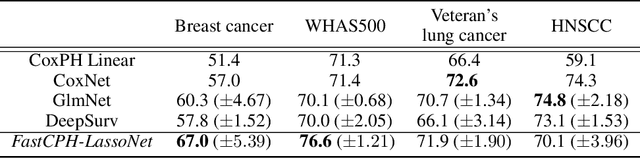
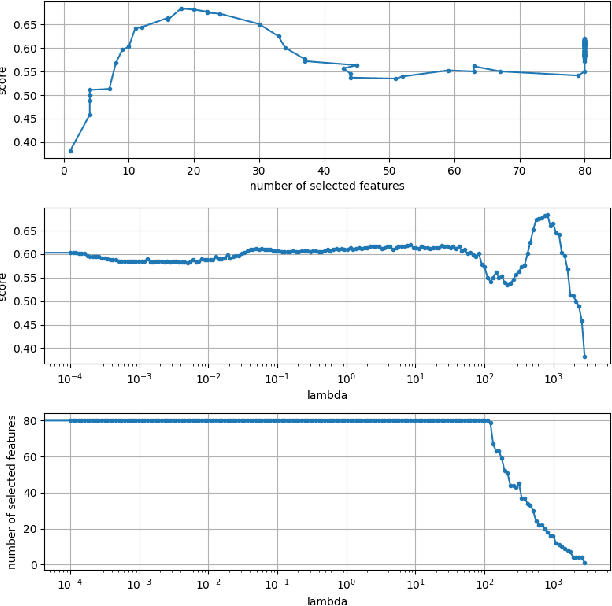
The Cox proportional hazards model is a canonical method in survival analysis for prediction of the life expectancy of a patient given clinical or genetic covariates -- it is a linear model in its original form. In recent years, several methods have been proposed to generalize the Cox model to neural networks, but none of these are both numerically correct and computationally efficient. We propose FastCPH, a new method that runs in linear time and supports both the standard Breslow and Efron methods for tied events. We also demonstrate the performance of FastCPH combined with LassoNet, a neural network that provides interpretability through feature sparsity, on survival datasets. The final procedure is efficient, selects useful covariates and outperforms existing CoxPH approaches.

ZeroC: A Neuro-Symbolic Model for Zero-shot Concept Recognition and Acquisition at Inference Time

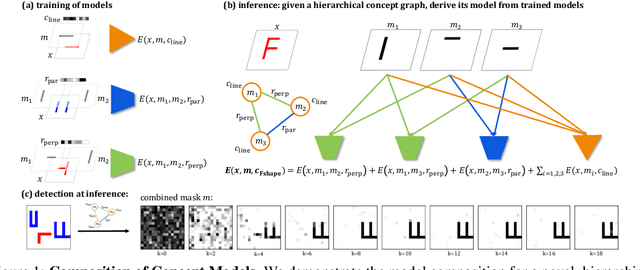
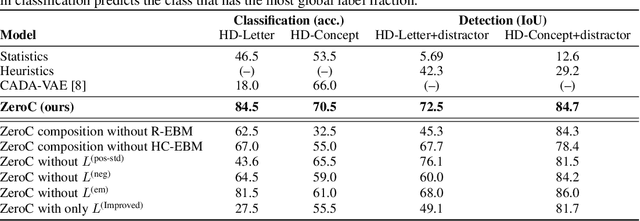
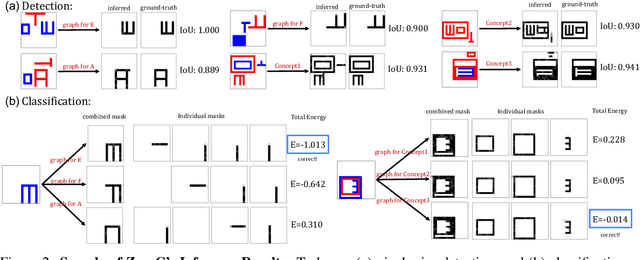
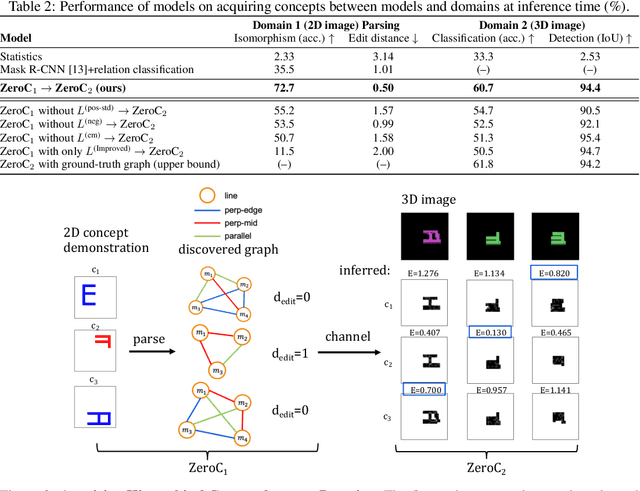
Humans have the remarkable ability to recognize and acquire novel visual concepts in a zero-shot manner. Given a high-level, symbolic description of a novel concept in terms of previously learned visual concepts and their relations, humans can recognize novel concepts without seeing any examples. Moreover, they can acquire new concepts by parsing and communicating symbolic structures using learned visual concepts and relations. Endowing these capabilities in machines is pivotal in improving their generalization capability at inference time. In this work, we introduce Zero-shot Concept Recognition and Acquisition (ZeroC), a neuro-symbolic architecture that can recognize and acquire novel concepts in a zero-shot way. ZeroC represents concepts as graphs of constituent concept models (as nodes) and their relations (as edges). To allow inference time composition, we employ energy-based models (EBMs) to model concepts and relations. We design ZeroC architecture so that it allows a one-to-one mapping between a symbolic graph structure of a concept and its corresponding EBM, which for the first time, allows acquiring new concepts, communicating its graph structure, and applying it to classification and detection tasks (even across domains) at inference time. We introduce algorithms for learning and inference with ZeroC. We evaluate ZeroC on a challenging grid-world dataset which is designed to probe zero-shot concept recognition and acquisition, and demonstrate its capability.