A General Bayesian Framework for Informative Input Design in System Identification

We tackle the problem of informative input design for system identification, where we select inputs, observe the corresponding outputs from the true system, and optimize the parameters of our model to best fit the data. We propose a methodology that is compatible with any system and parametric family of models. Our approach only requires input-output data from the system and first-order information from the model with respect to the parameters. Our algorithm consists of two modules. First, we formulate the problem of system identification from a Bayesian perspective and propose an approximate iterative method to optimize the model's parameters. Based on this Bayesian formulation, we are able to define a Gaussian-based uncertainty measure for the model parameters, which we can then minimize with respect to the next selected input. Our method outperforms model-free baselines with various linear and nonlinear dynamics.

Enhanced Importance Sampling through Latent Space Exploration in Normalizing Flows

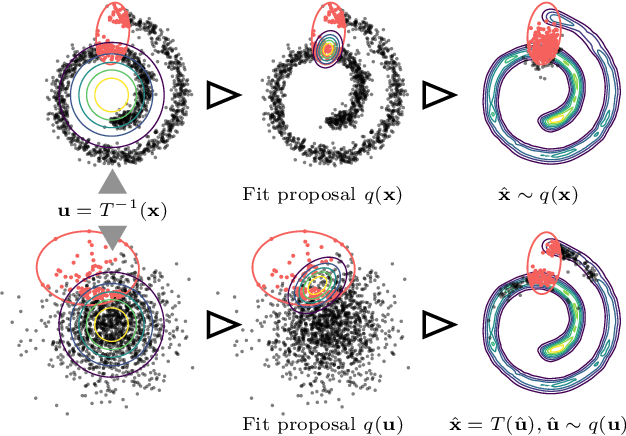
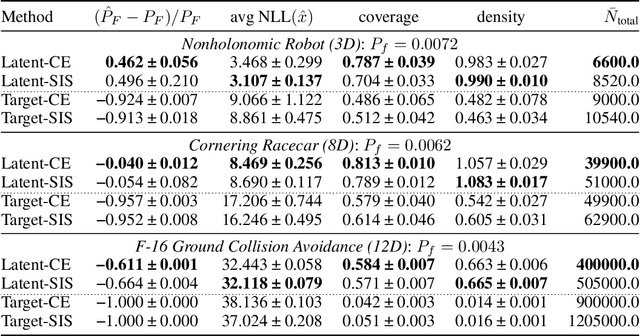
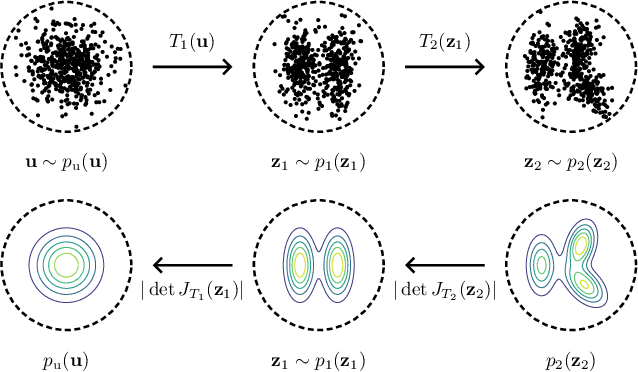
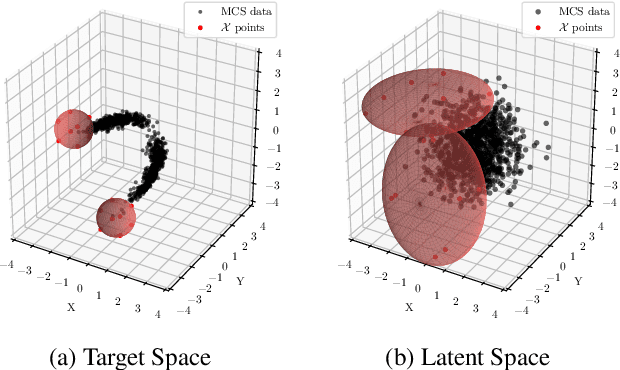
Importance sampling is a rare event simulation technique used in Monte Carlo simulations to bias the sampling distribution towards the rare event of interest. By assigning appropriate weights to sampled points, importance sampling allows for more efficient estimation of rare events or tails of distributions. However, importance sampling can fail when the proposal distribution does not effectively cover the target distribution. In this work, we propose a method for more efficient sampling by updating the proposal distribution in the latent space of a normalizing flow. Normalizing flows learn an invertible mapping from a target distribution to a simpler latent distribution. The latent space can be more easily explored during the search for a proposal distribution, and samples from the proposal distribution are recovered in the space of the target distribution via the invertible mapping. We empirically validate our methodology on simulated robotics applications such as autonomous racing and aircraft ground collision avoidance.

Discrete-Time Distribution Steering using Monte Carlo Tree Search

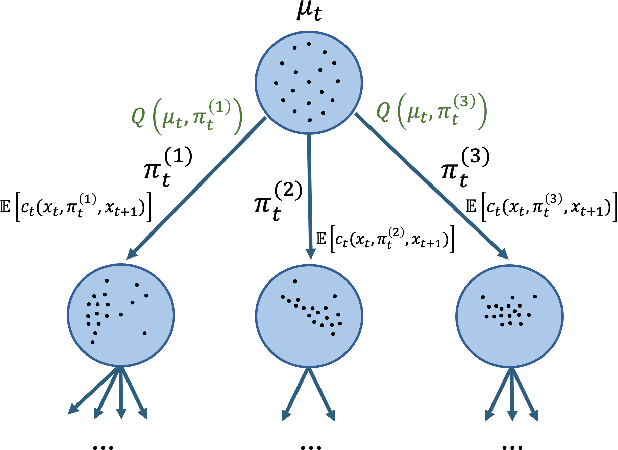
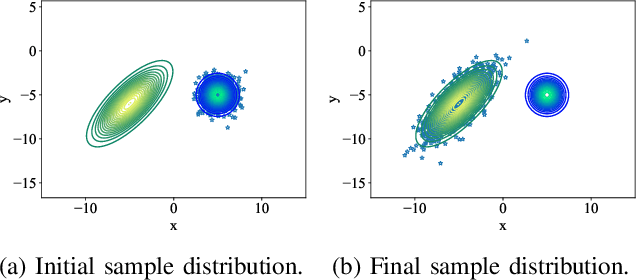
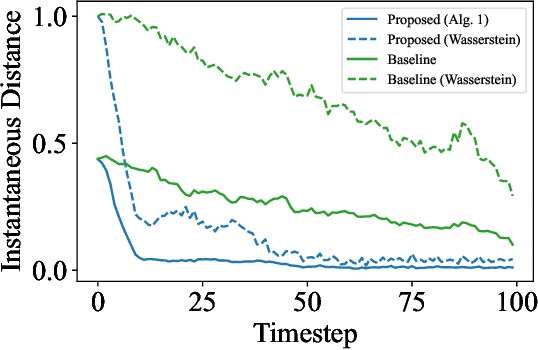
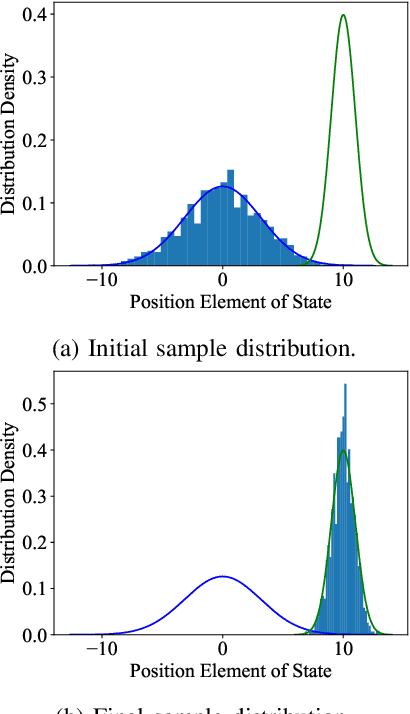
Optimal control problems with state distribution constraints have attracted interest for their expressivity, but solutions rely on linear approximations. We approach the problem of driving the state of a dynamical system in distribution from a sequential decision-making perspective. We formulate the optimal control problem as an appropriate Markov decision process (MDP), where the actions correspond to the state-feedback control policies. We then solve the MDP using Monte Carlo tree search (MCTS). This renders our method suitable for any dynamics model. A key component of our approach is a novel, easy to compute, distance metric in the distribution space that allows our algorithm to guide the distribution of the state. We experimentally test our algorithm under both linear and nonlinear dynamics.

Distributed Online Planning for Min-Max Problems in Networked Markov Games

Min-max problems are important in multi-agent sequential decision-making because they improve the performance of the worst-performing agent in the network. However, solving the multi-agent min-max problem is challenging. We propose a modular, distributed, online planning-based algorithm that is able to approximate the solution of the min-max objective in networked Markov games, assuming that the agents communicate within a network topology and the transition and reward functions are neighborhood-dependent. This set-up is encountered in the multi-robot setting. Our method consists of two phases at every planning step. In the first phase, each agent obtains sample returns based on its local reward function, by performing online planning. Using the samples from online planning, each agent constructs a concave approximation of its underlying local return as a function of only the action of its neighborhood at the next planning step. In the second phase, the agents deploy a distributed optimization framework that converges to the optimal immediate next action for each agent, based on the function approximations of the first phase. We demonstrate our algorithm's performance through formation control simulations.

Distributed Markov Chain Monte Carlo Sampling based on the Alternating Direction Method of Multipliers

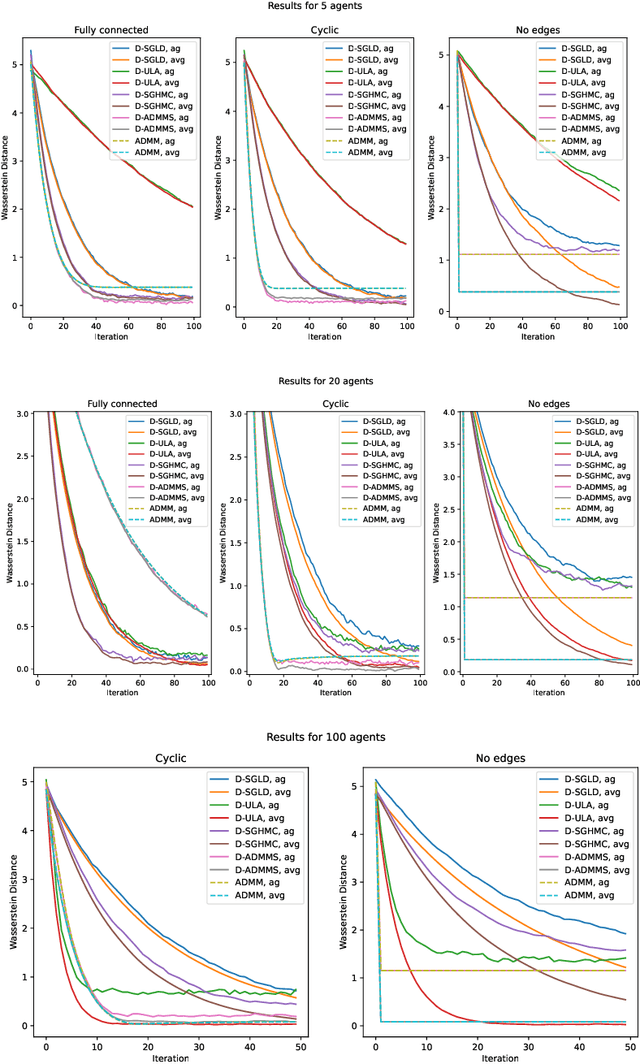
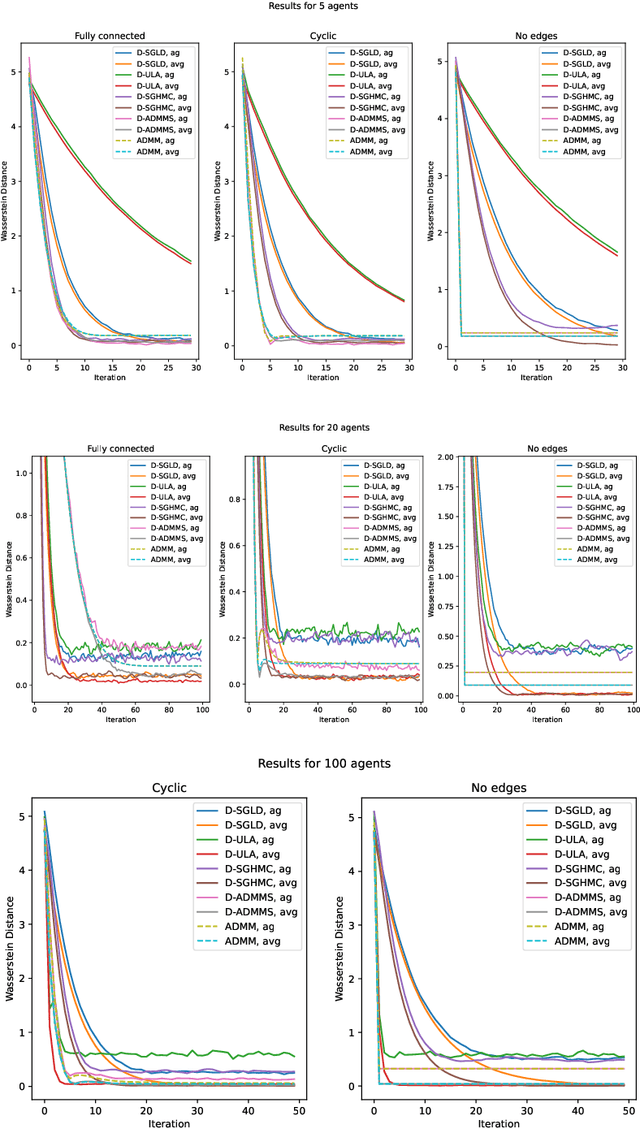
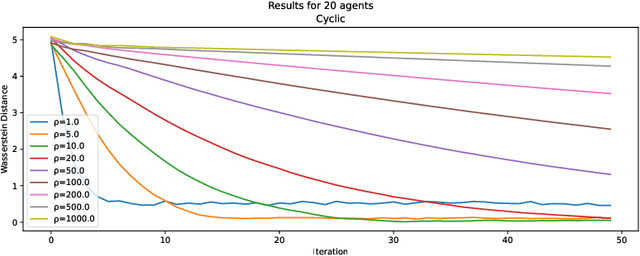
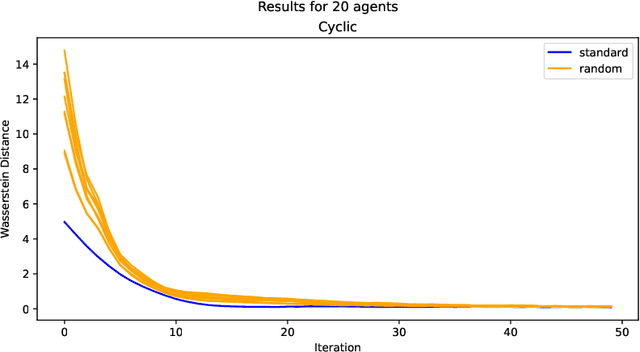
Many machine learning applications require operating on a spatially distributed dataset. Despite technological advances, privacy considerations and communication constraints may prevent gathering the entire dataset in a central unit. In this paper, we propose a distributed sampling scheme based on the alternating direction method of multipliers, which is commonly used in the optimization literature due to its fast convergence. In contrast to distributed optimization, distributed sampling allows for uncertainty quantification in Bayesian inference tasks. We provide both theoretical guarantees of our algorithm's convergence and experimental evidence of its superiority to the state-of-the-art. For our theoretical results, we use convex optimization tools to establish a fundamental inequality on the generated local sample iterates. This inequality enables us to show convergence of the distribution associated with these iterates to the underlying target distribution in Wasserstein distance. In simulation, we deploy our algorithm on linear and logistic regression tasks and illustrate its fast convergence compared to existing gradient-based methods.