Approximate Sequential Optimization for Informative Path Planning
Paper and Code
Feb 13, 2024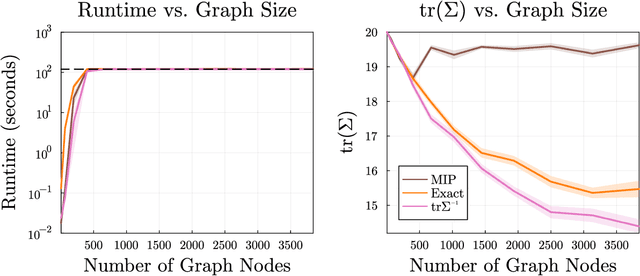
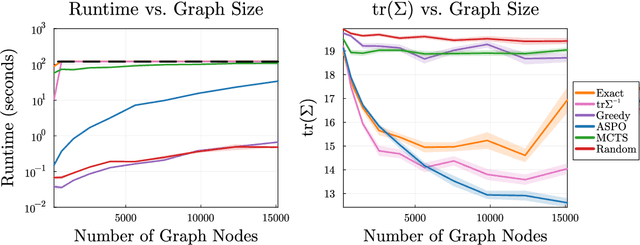
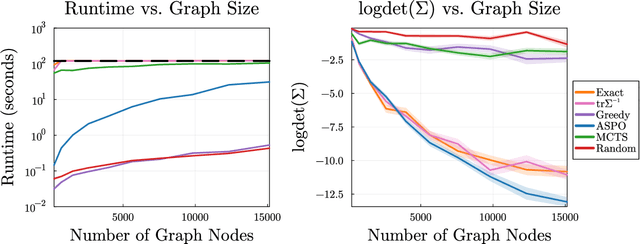
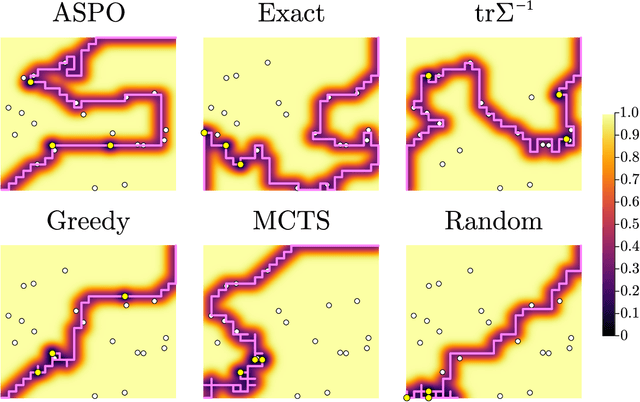
We consider the problem of finding an informative path through a graph, given initial and terminal nodes and a given maximum path length. We assume that a linear noise corrupted measurement is taken at each node of an underlying unknown vector that we wish to estimate. The informativeness is measured by the reduction in uncertainty in our estimate, evaluated using several metrics. We present a convex relaxation for this informative path planning problem, which we can readily solve to obtain a bound on the possible performance. We develop an approximate sequential method where the path is constructed segment by segment through dynamic programming. This involves solving an orienteering problem, with the node reward acting as a surrogate for informativeness, taking the first step, and then repeating the process. The method scales to very large problem instances and achieves performance not too far from the bound produced by the convex relaxation. We also demonstrate our method's ability to handle adaptive objectives, multimodal sensing, and multi-agent variations of the informative path planning problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge