Large-Scale GNSS Spreading Code Optimization

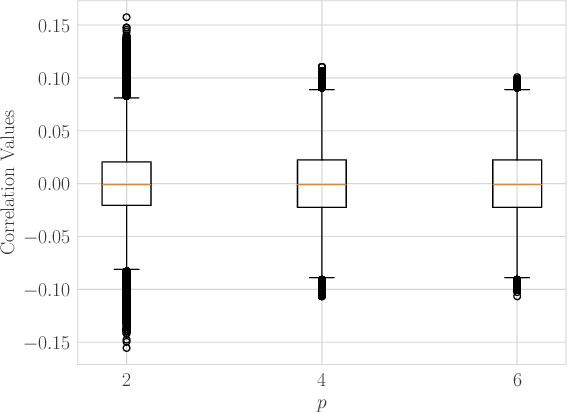
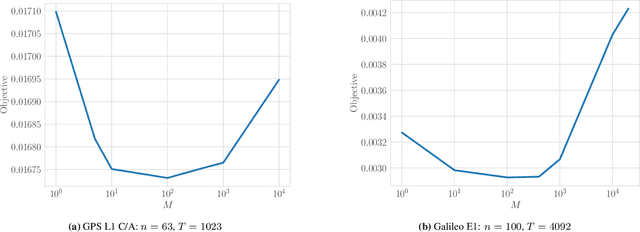
We propose a bit-flip descent method for optimizing binary spreading codes with large family sizes and long lengths, addressing the challenges of large-scale code design in GNSS and emerging PNT applications. The method iteratively flips code bits to improve the codes' auto- and cross-correlation properties. In our proposed method, bits are selected by sampling a small set of candidate bits and choosing the one that offers the best improvement in performance. The method leverages the fact that incremental impact of a bit flip on the auto- and cross-correlation may be efficiently computed without recalculating the entire function. We apply this method to two code design problems modeled after the GPS L1 C/A and Galileo E1 codes, demonstrating rapid convergence to low-correlation codes. The proposed approach offers a powerful tool for developing spreading codes that meet the demanding requirements of modern and future satellite navigation systems.

Spreading Code Optimization for Low-Earth Orbit Satellites via Mixed-Integer Convex Programming

Optimizing the correlation properties of spreading codes is critical for minimizing inter-channel interference in satellite navigation systems. By improving the codes' correlation sidelobes, we can enhance navigation performance while minimizing the required spreading code lengths. In the case of low earth orbit (LEO) satellite navigation, shorter code lengths (on the order of a hundred) are preferred due to their ability to achieve fast signal acquisition. Additionally, the relatively high signal-to-noise ratio (SNR) in LEO systems reduces the need for longer spreading codes to mitigate inter-channel interference. In this work, we propose a two-stage block coordinate descent (BCD) method which optimizes the codes' correlation properties while enforcing the autocorrelation sidelobe zero (ACZ) property. In each iteration of the BCD method, we solve a mixed-integer convex program (MICP) over a block of 25 binary variables. Our method is applicable to spreading code families of arbitrary sizes and lengths, and we demonstrate its effectiveness for a problem with 66 length-127 codes and a problem with 130 length-257 codes.

Binary sequence set optimization for CDMA applications via mixed-integer quadratic programming

Finding sets of binary sequences with low auto- and cross-correlation properties is a hard combinatorial optimization problem with numerous applications, including multiple-input-multiple-output (MIMO) radar and global navigation satellite systems (GNSS). The sum of squared correlations, also known as the integrated sidelobe level (ISL), is a quartic function in the variables and is a commonly-used metric of sequence set quality. In this paper, we show that the ISL minimization problem may be formulated as a mixed-integer quadratic program (MIQP). We then present a block coordinate descent (BCD) algorithm that iteratively optimizes over subsets of variables. The subset optimization subproblems are also MIQPs which may be handled more efficiently using specialized solvers than using brute-force search; this allows us to perform BCD over larger variable subsets than previously possible. Our approach was used to find sets of four binary sequences of lengths up to 1023 with better ISL performance than Gold codes and sequence sets found using existing BCD methods.

Input-to-State Stable Neural Ordinary Differential Equations with Applications to Transient Modeling of Circuits

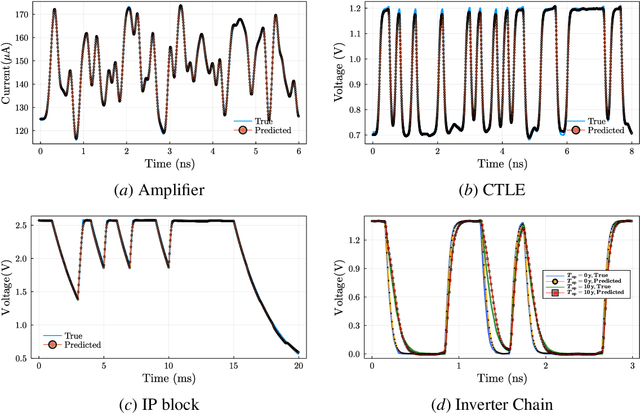
This paper proposes a class of neural ordinary differential equations parametrized by provably input-to-state stable continuous-time recurrent neural networks. The model dynamics are defined by construction to be input-to-state stable (ISS) with respect to an ISS-Lyapunov function that is learned jointly with the dynamics. We use the proposed method to learn cheap-to-simulate behavioral models for electronic circuits that can accurately reproduce the behavior of various digital and analog circuits when simulated by a commercial circuit simulator, even when interconnected with circuit components not encountered during training. We also demonstrate the feasibility of learning ISS-preserving perturbations to the dynamics for modeling degradation effects due to circuit aging.

Model-Augmented Nearest-Neighbor Estimation of Conditional Mutual Information for Feature Selection

Markov blanket feature selection, while theoretically optimal, generally is challenging to implement. This is due to the shortcomings of existing approaches to conditional independence (CI) testing, which tend to struggle either with the curse of dimensionality or computational complexity. We propose a novel two-step approach which facilitates Markov blanket feature selection in high dimensions. First, neural networks are used to map features to low-dimensional representations. In the second step, CI testing is performed by applying the k-NN conditional mutual information estimator to the learned feature maps. The mappings are designed to ensure that mapped samples both preserve information and share similar information about the target variable if and only if they are close in Euclidean distance. We show that these properties boost the performance of the k-NN estimator in the second step. The performance of the proposed method is evaluated on synthetic, as well as real data pertaining to datacenter hard disk drive failures.