Input-to-State Stable Neural Ordinary Differential Equations with Applications to Transient Modeling of Circuits

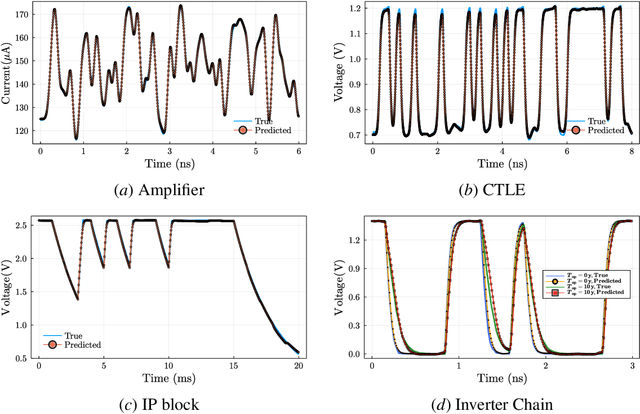
This paper proposes a class of neural ordinary differential equations parametrized by provably input-to-state stable continuous-time recurrent neural networks. The model dynamics are defined by construction to be input-to-state stable (ISS) with respect to an ISS-Lyapunov function that is learned jointly with the dynamics. We use the proposed method to learn cheap-to-simulate behavioral models for electronic circuits that can accurately reproduce the behavior of various digital and analog circuits when simulated by a commercial circuit simulator, even when interconnected with circuit components not encountered during training. We also demonstrate the feasibility of learning ISS-preserving perturbations to the dynamics for modeling degradation effects due to circuit aging.

Model-Augmented Nearest-Neighbor Estimation of Conditional Mutual Information for Feature Selection

Markov blanket feature selection, while theoretically optimal, generally is challenging to implement. This is due to the shortcomings of existing approaches to conditional independence (CI) testing, which tend to struggle either with the curse of dimensionality or computational complexity. We propose a novel two-step approach which facilitates Markov blanket feature selection in high dimensions. First, neural networks are used to map features to low-dimensional representations. In the second step, CI testing is performed by applying the k-NN conditional mutual information estimator to the learned feature maps. The mappings are designed to ensure that mapped samples both preserve information and share similar information about the target variable if and only if they are close in Euclidean distance. We show that these properties boost the performance of the k-NN estimator in the second step. The performance of the proposed method is evaluated on synthetic, as well as real data pertaining to datacenter hard disk drive failures.