Generative Diffusion Models for Lattice Field Theory
Paper and Code
Nov 06, 2023
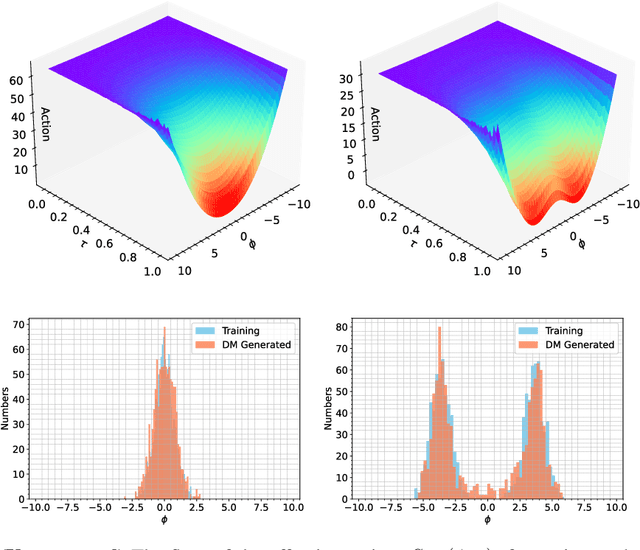
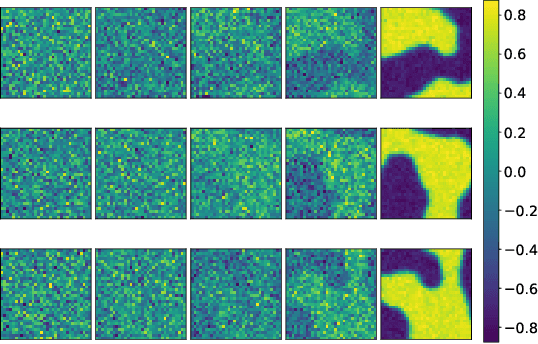
This study delves into the connection between machine learning and lattice field theory by linking generative diffusion models (DMs) with stochastic quantization, from a stochastic differential equation perspective. We show that DMs can be conceptualized by reversing a stochastic process driven by the Langevin equation, which then produces samples from an initial distribution to approximate the target distribution. In a toy model, we highlight the capability of DMs to learn effective actions. Furthermore, we demonstrate its feasibility to act as a global sampler for generating configurations in the two-dimensional $\phi^4$ quantum lattice field theory.
* 6 pages, 3 figures, accepted at the NeurIPS 2023 workshop "Machine
Learning and the Physical Sciences". Some contents overlap with
arXiv:2309.17082
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge