Biagio Lucini
Swansea University
Random Matrix Theory for Stochastic Gradient Descent
Dec 29, 2024Abstract:Investigating the dynamics of learning in machine learning algorithms is of paramount importance for understanding how and why an approach may be successful. The tools of physics and statistics provide a robust setting for such investigations. Here we apply concepts from random matrix theory to describe stochastic weight matrix dynamics, using the framework of Dyson Brownian motion. We derive the linear scaling rule between the learning rate (step size) and the batch size, and identify universal and non-universal aspects of weight matrix dynamics. We test our findings in the (near-)solvable case of the Gaussian Restricted Boltzmann Machine and in a linear one-hidden-layer neural network.
Dyson Brownian motion and random matrix dynamics of weight matrices during learning
Nov 20, 2024Abstract:During training, weight matrices in machine learning architectures are updated using stochastic gradient descent or variations thereof. In this contribution we employ concepts of random matrix theory to analyse the resulting stochastic matrix dynamics. We first demonstrate that the dynamics can generically be described using Dyson Brownian motion, leading to e.g. eigenvalue repulsion. The level of stochasticity is shown to depend on the ratio of the learning rate and the mini-batch size, explaining the empirically observed linear scaling rule. We verify this linear scaling in the restricted Boltzmann machine. Subsequently we study weight matrix dynamics in transformers (a nano-GPT), following the evolution from a Marchenko-Pastur distribution for eigenvalues at initialisation to a combination with additional structure at the end of learning.
Stochastic weight matrix dynamics during learning and Dyson Brownian motion
Jul 23, 2024Abstract:We demonstrate that the update of weight matrices in learning algorithms can be described in the framework of Dyson Brownian motion, thereby inheriting many features of random matrix theory. We relate the level of stochasticity to the ratio of the learning rate and the mini-batch size, providing more robust evidence to a previously conjectured scaling relationship. We discuss universal and non-universal features in the resulting Coulomb gas distribution and identify the Wigner surmise and Wigner semicircle explicitly in a teacher-student model and in the (near-)solvable case of the Gaussian restricted Boltzmann machine.
Applications of Machine Learning to Lattice Quantum Field Theory
Feb 10, 2022Abstract:There is great potential to apply machine learning in the area of numerical lattice quantum field theory, but full exploitation of that potential will require new strategies. In this white paper for the Snowmass community planning process, we discuss the unique requirements of machine learning for lattice quantum field theory research and outline what is needed to enable exploration and deployment of this approach in the future.
Quantum field theories, Markov random fields and machine learning
Oct 21, 2021



Abstract:The transition to Euclidean space and the discretization of quantum field theories on spatial or space-time lattices opens up the opportunity to investigate probabilistic machine learning from the perspective of quantum field theory. Here, we will discuss how discretized Euclidean field theories can be recast within the mathematical framework of Markov random fields, which is a notable class of probabilistic graphical models with applications in a variety of research areas, including machine learning. Specifically, we will demonstrate that the $\phi^{4}$ scalar field theory on a square lattice satisfies the Hammersley-Clifford theorem, therefore recasting it as a Markov random field from which neural networks are additionally derived. We will then discuss applications pertinent to the minimization of an asymmetric distance between the probability distribution of the $\phi^{4}$ machine learning algorithms and that of target probability distributions.
Quantitative analysis of phase transitions in two-dimensional XY models using persistent homology
Sep 22, 2021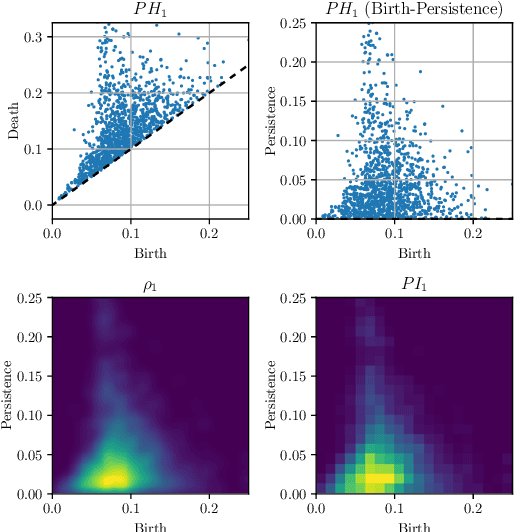
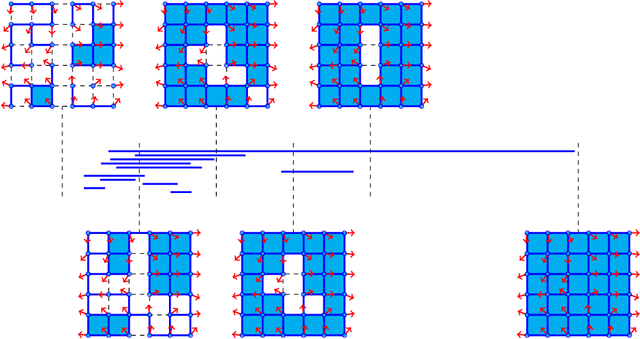
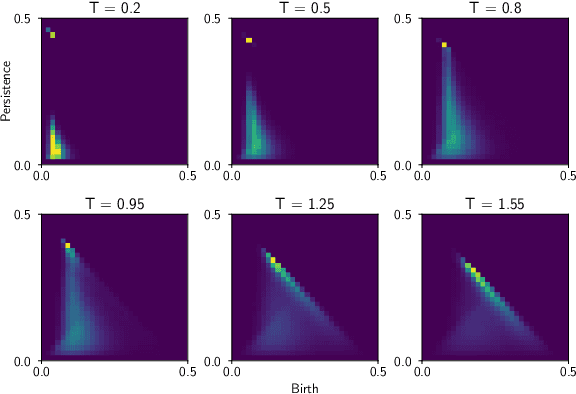
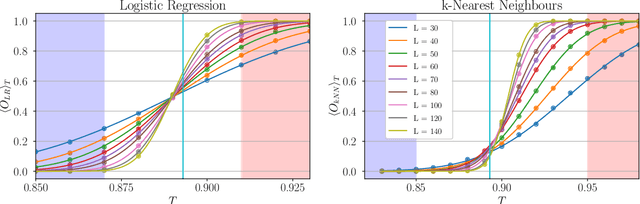
Abstract:We use persistent homology and persistence images as an observable of three different variants of the two-dimensional XY model in order to identify and study their phase transitions. We examine models with the classical XY action, a topological lattice action, and an action with an additional nematic term. In particular, we introduce a new way of computing the persistent homology of lattice spin model configurations and, by considering the fluctuations in the output of logistic regression and k-nearest neighbours models trained on persistence images, we develop a methodology to extract estimates of the critical temperature and the critical exponent of the correlation length. We put particular emphasis on finite-size scaling behaviour and producing estimates with quantifiable error. For each model we successfully identify its phase transition(s) and are able to get an accurate determination of the critical temperatures and critical exponents of the correlation length.
Machine learning with quantum field theories
Sep 16, 2021


Abstract:The precise equivalence between discretized Euclidean field theories and a certain class of probabilistic graphical models, namely the mathematical framework of Markov random fields, opens up the opportunity to investigate machine learning from the perspective of quantum field theory. In this contribution we will demonstrate, through the Hammersley-Clifford theorem, that the $\phi^{4}$ scalar field theory on a square lattice satisfies the local Markov property and can therefore be recast as a Markov random field. We will then derive from the $\phi^{4}$ theory machine learning algorithms and neural networks which can be viewed as generalizations of conventional neural network architectures. Finally, we will conclude by presenting applications based on the minimization of an asymmetric distance between the probability distribution of the $\phi^{4}$ machine learning algorithms and target probability distributions.
Quantum field-theoretic machine learning
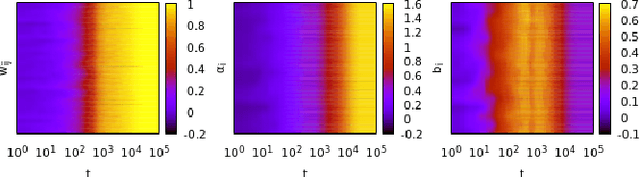
Feb 18, 2021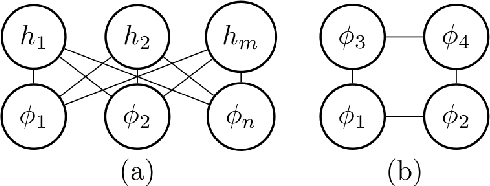
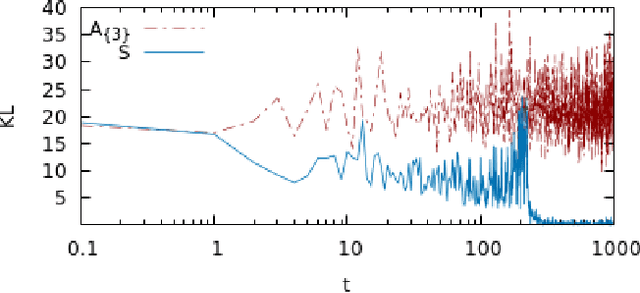

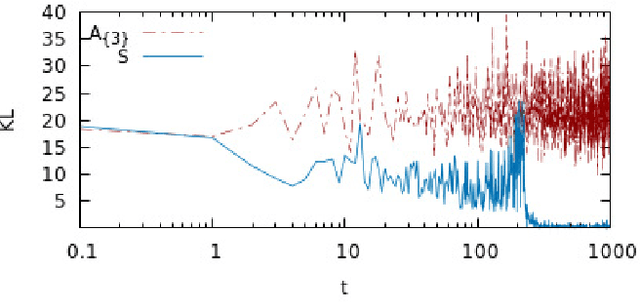
Abstract:We derive machine learning algorithms from discretized Euclidean field theories, making inference and learning possible within dynamics described by quantum field theory. Specifically, we demonstrate that the $\phi^{4}$ scalar field theory satisfies the Hammersley-Clifford theorem, therefore recasting it as a machine learning algorithm within the mathematically rigorous framework of Markov random fields. We illustrate the concepts by minimizing an asymmetric distance between the probability distribution of the $\phi^{4}$ theory and that of target distributions, by quantifying the overlap of statistical ensembles between probability distributions and through reweighting to complex-valued actions with longer-range interactions. Neural networks architectures are additionally derived from the $\phi^{4}$ theory which can be viewed as generalizations of conventional neural networks and applications are presented. We conclude by discussing how the proposal opens up a new research avenue, that of developing a mathematical and computational framework of machine learning within quantum field theory.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge