Applications of Lattice Gauge Equivariant Neural Networks

The introduction of relevant physical information into neural network architectures has become a widely used and successful strategy for improving their performance. In lattice gauge theories, such information can be identified with gauge symmetries, which are incorporated into the network layers of our recently proposed Lattice Gauge Equivariant Convolutional Neural Networks (L-CNNs). L-CNNs can generalize better to differently sized lattices than traditional neural networks and are by construction equivariant under lattice gauge transformations. In these proceedings, we present our progress on possible applications of L-CNNs to Wilson flow or continuous normalizing flow. Our methods are based on neural ordinary differential equations which allow us to modify link configurations in a gauge equivariant manner. For simplicity, we focus on simple toy models to test these ideas in practice.

Equivariance and generalization in neural networks

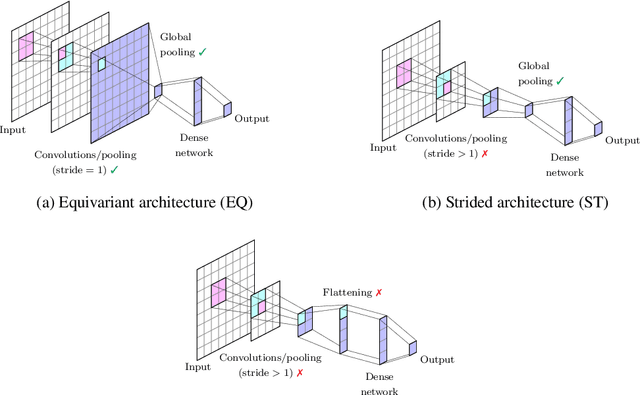
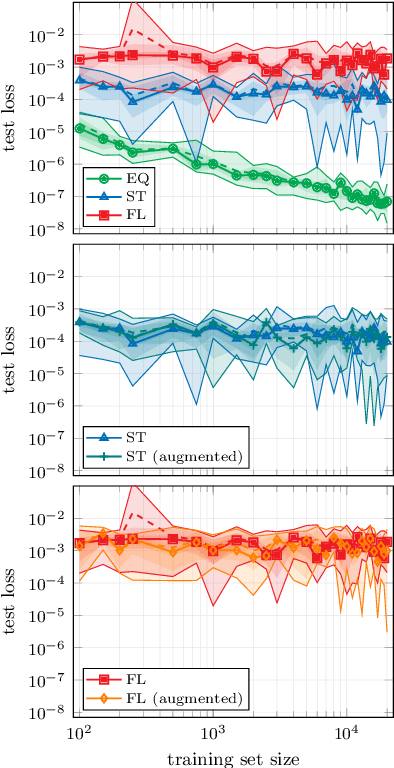
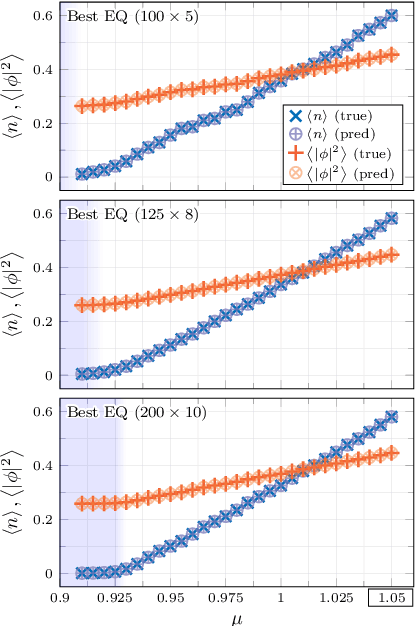
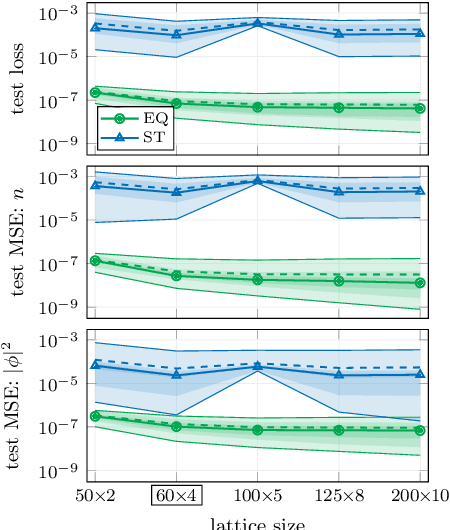
The crucial role played by the underlying symmetries of high energy physics and lattice field theories calls for the implementation of such symmetries in the neural network architectures that are applied to the physical system under consideration. In these proceedings, we focus on the consequences of incorporating translational equivariance among the network properties, particularly in terms of performance and generalization. The benefits of equivariant networks are exemplified by studying a complex scalar field theory, on which various regression and classification tasks are examined. For a meaningful comparison, promising equivariant and non-equivariant architectures are identified by means of a systematic search. The results indicate that in most of the tasks our best equivariant architectures can perform and generalize significantly better than their non-equivariant counterparts, which applies not only to physical parameters beyond those represented in the training set, but also to different lattice sizes.

Generalization capabilities of neural networks in lattice applications

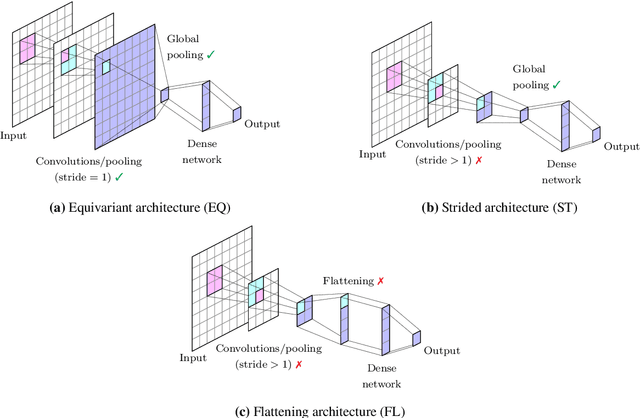
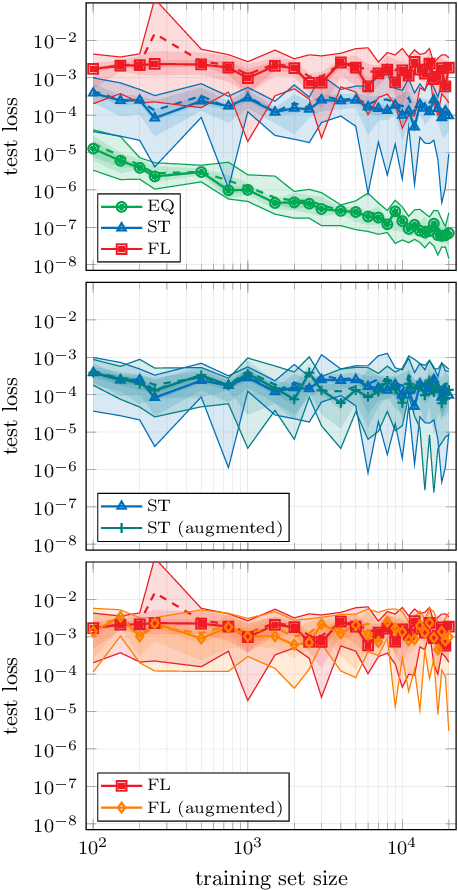
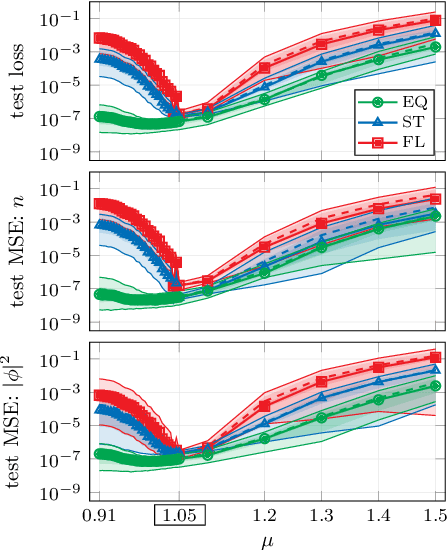
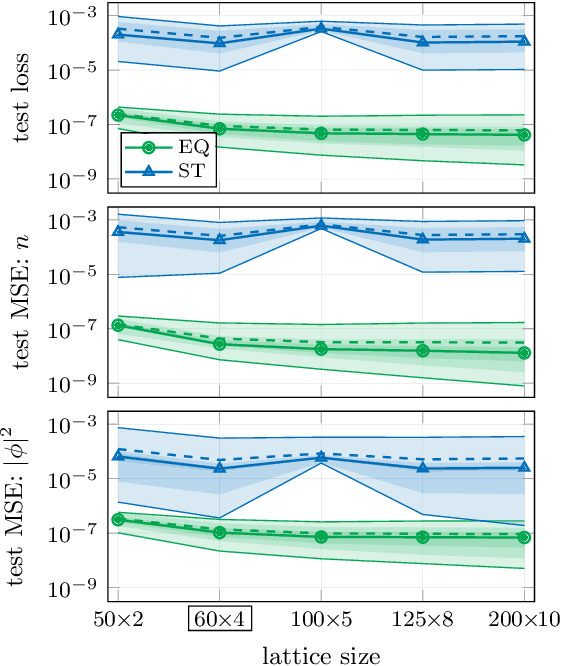
In recent years, the use of machine learning has become increasingly popular in the context of lattice field theories. An essential element of such theories is represented by symmetries, whose inclusion in the neural network properties can lead to high reward in terms of performance and generalizability. A fundamental symmetry that usually characterizes physical systems on a lattice with periodic boundary conditions is equivariance under spacetime translations. Here we investigate the advantages of adopting translationally equivariant neural networks in favor of non-equivariant ones. The system we consider is a complex scalar field with quartic interaction on a two-dimensional lattice in the flux representation, on which the networks carry out various regression and classification tasks. Promising equivariant and non-equivariant architectures are identified with a systematic search. We demonstrate that in most of these tasks our best equivariant architectures can perform and generalize significantly better than their non-equivariant counterparts, which applies not only to physical parameters beyond those represented in the training set, but also to different lattice sizes.

Preserving gauge invariance in neural networks

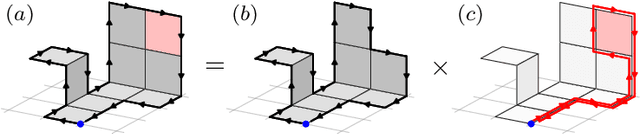
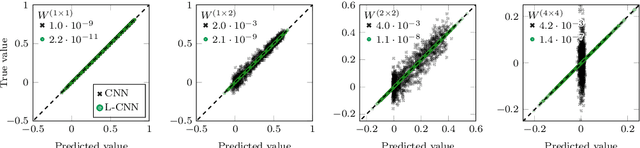
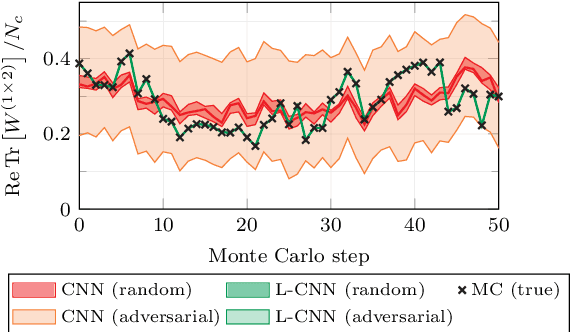
In these proceedings we present lattice gauge equivariant convolutional neural networks (L-CNNs) which are able to process data from lattice gauge theory simulations while exactly preserving gauge symmetry. We review aspects of the architecture and show how L-CNNs can represent a large class of gauge invariant and equivariant functions on the lattice. We compare the performance of L-CNNs and non-equivariant networks using a non-linear regression problem and demonstrate how gauge invariance is broken for non-equivariant models.

Lattice gauge symmetry in neural networks

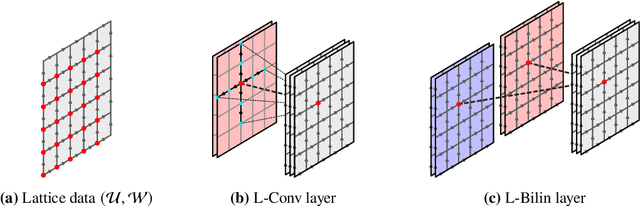
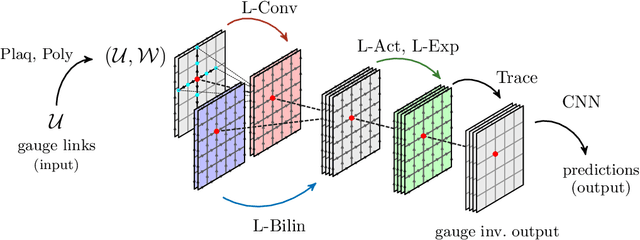
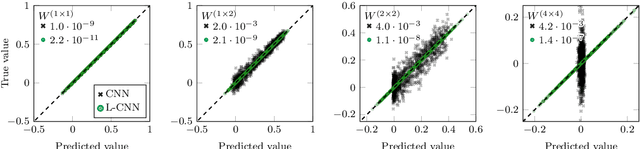
We review a novel neural network architecture called lattice gauge equivariant convolutional neural networks (L-CNNs), which can be applied to generic machine learning problems in lattice gauge theory while exactly preserving gauge symmetry. We discuss the concept of gauge equivariance which we use to explicitly construct a gauge equivariant convolutional layer and a bilinear layer. The performance of L-CNNs and non-equivariant CNNs is compared using seemingly simple non-linear regression tasks, where L-CNNs demonstrate generalizability and achieve a high degree of accuracy in their predictions compared to their non-equivariant counterparts.

Generalization capabilities of translationally equivariant neural networks

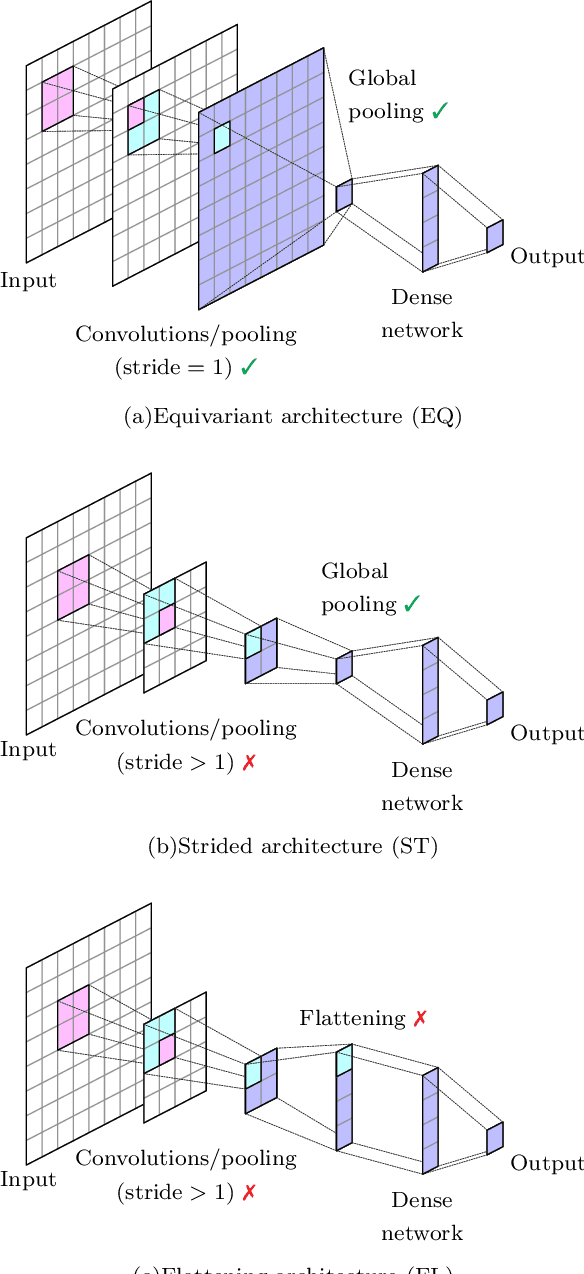
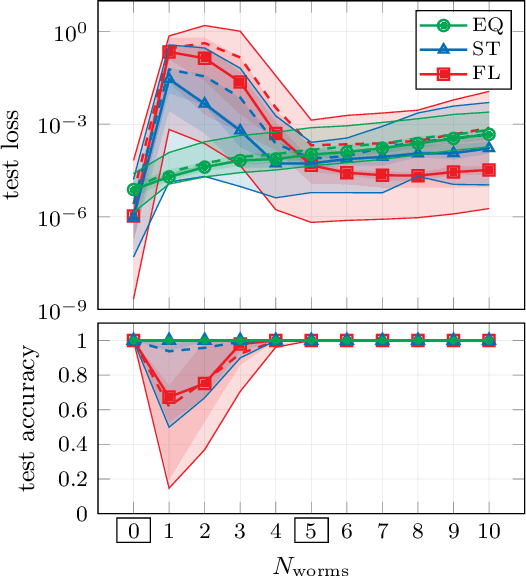
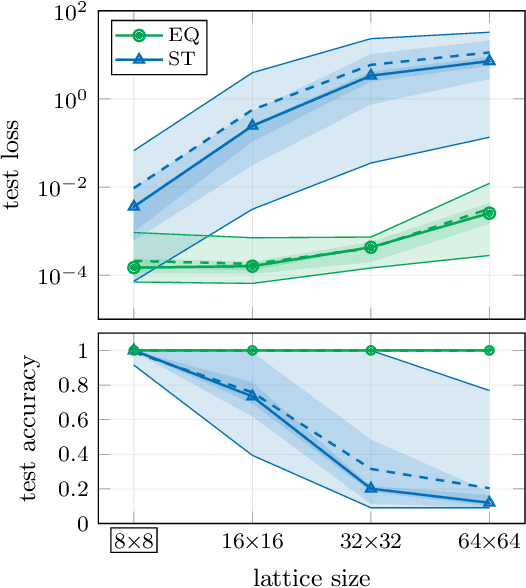
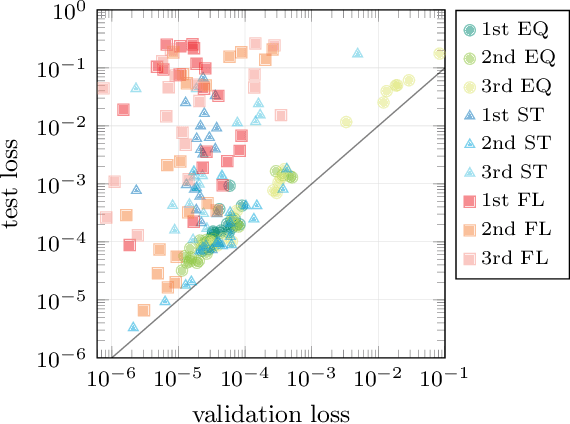
The rising adoption of machine learning in high energy physics and lattice field theory necessitates the re-evaluation of common methods that are widely used in computer vision, which, when applied to problems in physics, can lead to significant drawbacks in terms of performance and generalizability. One particular example for this is the use of neural network architectures that do not reflect the underlying symmetries of the given physical problem. In this work, we focus on complex scalar field theory on a two-dimensional lattice and investigate the benefits of using group equivariant convolutional neural network architectures based on the translation group. For a meaningful comparison, we conduct a systematic search for equivariant and non-equivariant neural network architectures and apply them to various regression and classification tasks. We demonstrate that in most of these tasks our best equivariant architectures can perform and generalize significantly better than their non-equivariant counterparts, which applies not only to physical parameters beyond those represented in the training set, but also to different lattice sizes.

Lattice gauge equivariant convolutional neural networks

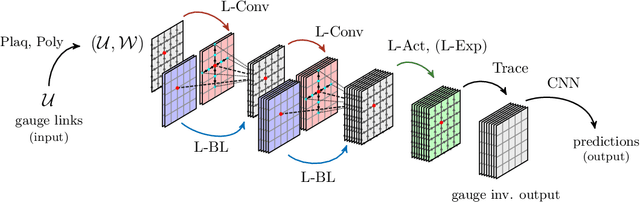
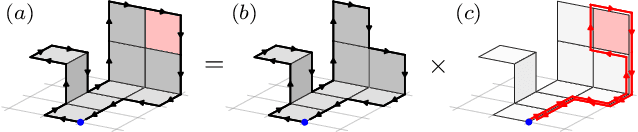
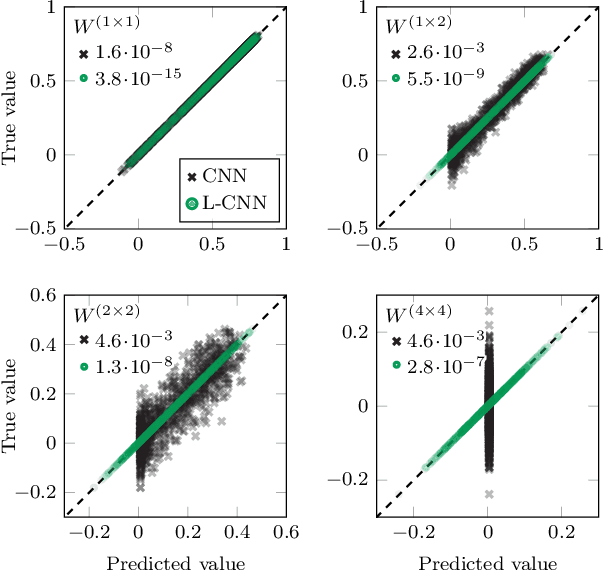
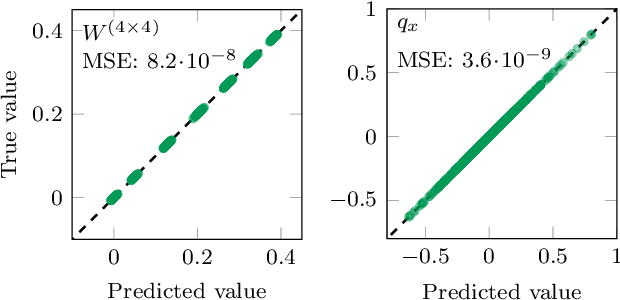
We propose Lattice gauge equivariant Convolutional Neural Networks (L-CNNs) for generic machine learning applications on lattice gauge theoretical problems. At the heart of this network structure is a novel convolutional layer that preserves gauge equivariance while forming arbitrarily shaped Wilson loops in successive bilinear layers. Together with topological information, for example from Polyakov loops, such a network can in principle approximate any gauge covariant function on the lattice. We demonstrate that L-CNNs can learn and generalize gauge invariant quantities that traditional convolutional neural networks are incapable of finding.