Lattice gauge equivariant convolutional neural networks
Paper and Code
Dec 23, 2020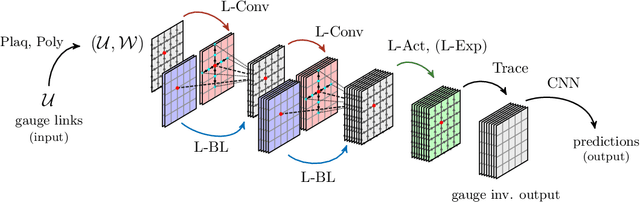
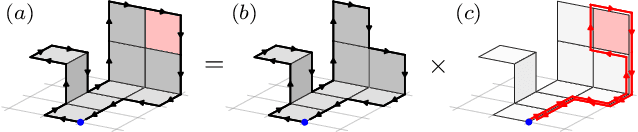
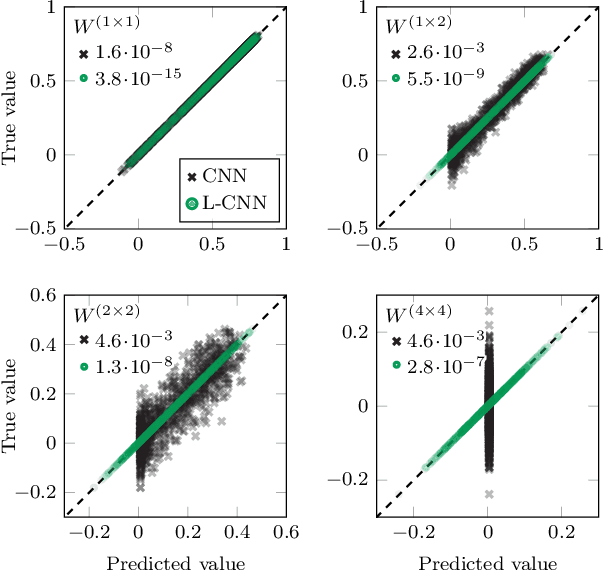
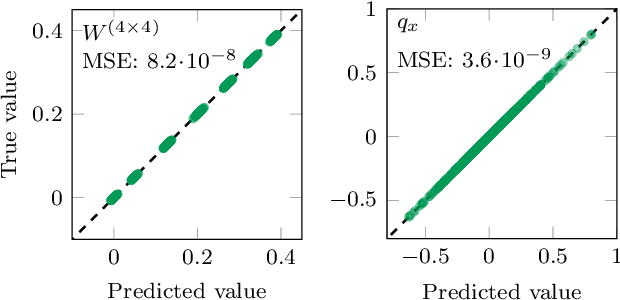
We propose Lattice gauge equivariant Convolutional Neural Networks (L-CNNs) for generic machine learning applications on lattice gauge theoretical problems. At the heart of this network structure is a novel convolutional layer that preserves gauge equivariance while forming arbitrarily shaped Wilson loops in successive bilinear layers. Together with topological information, for example from Polyakov loops, such a network can in principle approximate any gauge covariant function on the lattice. We demonstrate that L-CNNs can learn and generalize gauge invariant quantities that traditional convolutional neural networks are incapable of finding.
* 6 pages, 4 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge