Preserving gauge invariance in neural networks
Paper and Code
Dec 21, 2021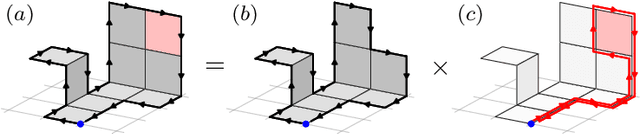
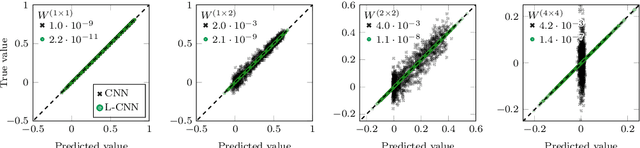
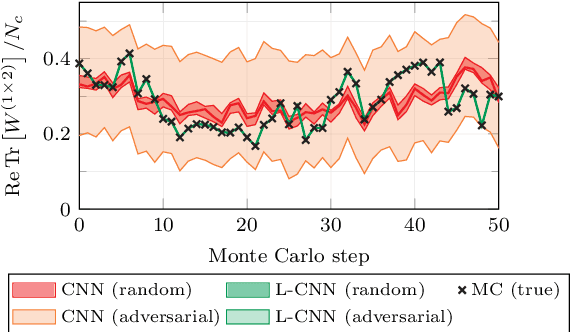
In these proceedings we present lattice gauge equivariant convolutional neural networks (L-CNNs) which are able to process data from lattice gauge theory simulations while exactly preserving gauge symmetry. We review aspects of the architecture and show how L-CNNs can represent a large class of gauge invariant and equivariant functions on the lattice. We compare the performance of L-CNNs and non-equivariant networks using a non-linear regression problem and demonstrate how gauge invariance is broken for non-equivariant models.
* 8 pages, 3 figures, proceedings for vConf 2021
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge