Lattice $φ^{4}$ field theory as a multi-agent system of financial markets

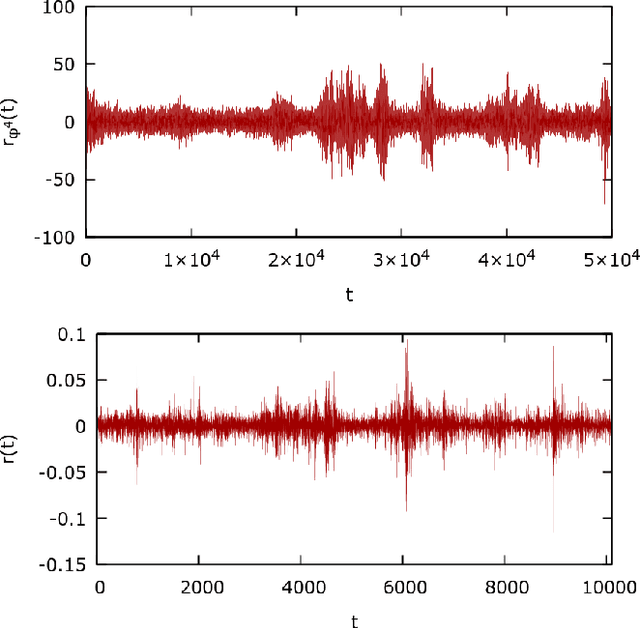
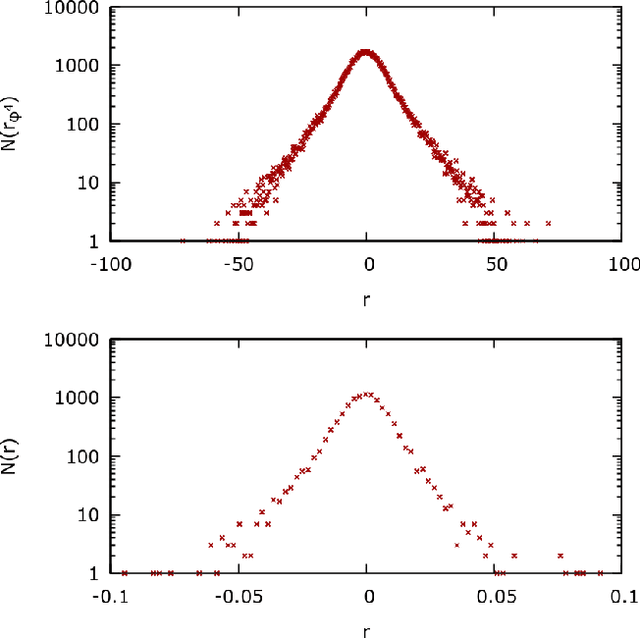
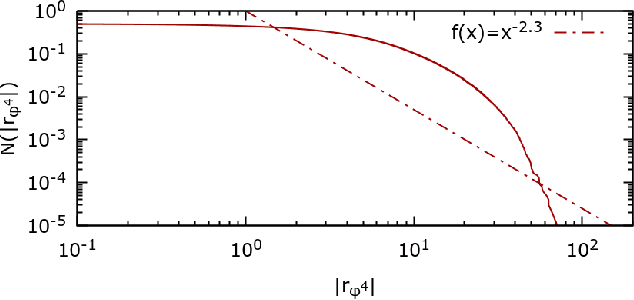
We introduce a $\phi^{4}$ lattice field theory with frustrated dynamics as a multi-agent system to reproduce stylized facts of financial markets such as fat-tailed distributions of returns and clustered volatility. Each lattice site, represented by a continuous degree of freedom, corresponds to an agent experiencing a set of competing interactions which influence its decision to buy or sell a given stock. These interactions comprise a cooperative term, which signifies that the agent should imitate the behavior of its neighbors, and a fictitious field, which compels the agent instead to conform with the opinion of the majority or the minority. To introduce the competing dynamics we exploit the Markov field structure to pursue a constructive decomposition of the $\phi^{4}$ probability distribution which we recompose with a Ferrenberg-Swendsen acceptance or rejection sampling step. We then verify numerically that the multi-agent $\phi^{4}$ field theory produces behavior observed on empirical data from the FTSE 100 London Stock Exchange index. We conclude by discussing how the presence of continuous degrees of freedom within the $\phi^{4}$ lattice field theory enables a representational capacity beyond that possible with multi-agent systems derived from Ising models.

Generating configurations of increasing lattice size with machine learning and the inverse renormalization group

We review recent developments of machine learning algorithms pertinent to the inverse renormalization group, which was originally established as a generative numerical method by Ron-Swendsen-Brandt via the implementation of compatible Monte Carlo simulations. Inverse renormalization group methods enable the iterative generation of configurations for increasing lattice size without the critical slowing down effect. We discuss the construction of inverse renormalization group transformations with the use of convolutional neural networks and present applications in models of statistical mechanics, lattice field theory, and disordered systems. We highlight the case of the three-dimensional Edwards-Anderson spin glass, where the inverse renormalization group can be employed to construct configurations for lattice volumes that have not yet been accessed by dedicated supercomputers.

Cascade of phase transitions in the training of Energy-based models

In this paper, we investigate the feature encoding process in a prototypical energy-based generative model, the Restricted Boltzmann Machine (RBM). We start with an analytical investigation using simplified architectures and data structures, and end with numerical analysis of real trainings on real datasets. Our study tracks the evolution of the model's weight matrix through its singular value decomposition, revealing a series of phase transitions associated to a progressive learning of the principal modes of the empirical probability distribution. The model first learns the center of mass of the modes and then progressively resolve all modes through a cascade of phase transitions. We first describe this process analytically in a controlled setup that allows us to study analytically the training dynamics. We then validate our theoretical results by training the Bernoulli-Bernoulli RBM on real data sets. By using data sets of increasing dimension, we show that learning indeed leads to sharp phase transitions in the high-dimensional limit. Moreover, we propose and test a mean-field finite-size scaling hypothesis. This shows that the first phase transition is in the same universality class of the one we studied analytically, and which is reminiscent of the mean-field paramagnetic-to-ferromagnetic phase transition.

Inverse Renormalization Group of Disordered Systems

We propose inverse renormalization group transformations to construct approximate configurations for lattice volumes that have not yet been accessed by supercomputers or large-scale simulations in the study of spin glasses. Specifically, starting from lattices of volume $V=8^{3}$ in the case of the three-dimensional Edwards-Anderson model we employ machine learning algorithms to construct rescaled lattices up to $V'=128^{3}$, which we utilize to extract two critical exponents. We conclude by discussing how to incorporate numerical exactness within inverse renormalization group approaches of disordered systems, thus opening up the opportunity to explore a sustainable and energy-efficient generation of exact configurations for increasing lattice volumes without the use of dedicated supercomputers.

Quantum field theories, Markov random fields and machine learning

The transition to Euclidean space and the discretization of quantum field theories on spatial or space-time lattices opens up the opportunity to investigate probabilistic machine learning from the perspective of quantum field theory. Here, we will discuss how discretized Euclidean field theories can be recast within the mathematical framework of Markov random fields, which is a notable class of probabilistic graphical models with applications in a variety of research areas, including machine learning. Specifically, we will demonstrate that the $\phi^{4}$ scalar field theory on a square lattice satisfies the Hammersley-Clifford theorem, therefore recasting it as a Markov random field from which neural networks are additionally derived. We will then discuss applications pertinent to the minimization of an asymmetric distance between the probability distribution of the $\phi^{4}$ machine learning algorithms and that of target probability distributions.

Machine learning with quantum field theories

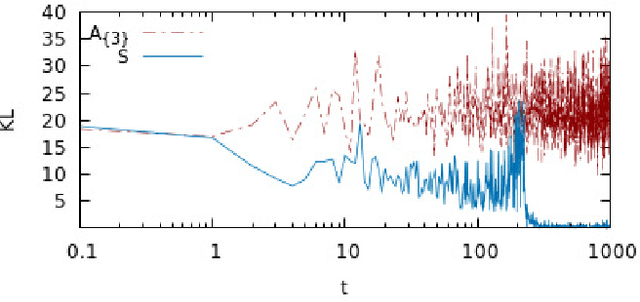
The precise equivalence between discretized Euclidean field theories and a certain class of probabilistic graphical models, namely the mathematical framework of Markov random fields, opens up the opportunity to investigate machine learning from the perspective of quantum field theory. In this contribution we will demonstrate, through the Hammersley-Clifford theorem, that the $\phi^{4}$ scalar field theory on a square lattice satisfies the local Markov property and can therefore be recast as a Markov random field. We will then derive from the $\phi^{4}$ theory machine learning algorithms and neural networks which can be viewed as generalizations of conventional neural network architectures. Finally, we will conclude by presenting applications based on the minimization of an asymmetric distance between the probability distribution of the $\phi^{4}$ machine learning algorithms and target probability distributions.

Quantum field-theoretic machine learning

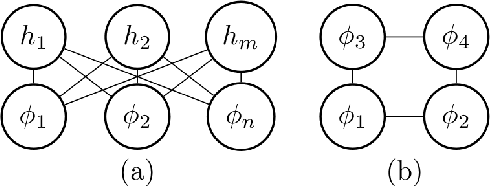
We derive machine learning algorithms from discretized Euclidean field theories, making inference and learning possible within dynamics described by quantum field theory. Specifically, we demonstrate that the $\phi^{4}$ scalar field theory satisfies the Hammersley-Clifford theorem, therefore recasting it as a machine learning algorithm within the mathematically rigorous framework of Markov random fields. We illustrate the concepts by minimizing an asymmetric distance between the probability distribution of the $\phi^{4}$ theory and that of target distributions, by quantifying the overlap of statistical ensembles between probability distributions and through reweighting to complex-valued actions with longer-range interactions. Neural networks architectures are additionally derived from the $\phi^{4}$ theory which can be viewed as generalizations of conventional neural networks and applications are presented. We conclude by discussing how the proposal opens up a new research avenue, that of developing a mathematical and computational framework of machine learning within quantum field theory.