Lattice $φ^{4}$ field theory as a multi-agent system of financial markets

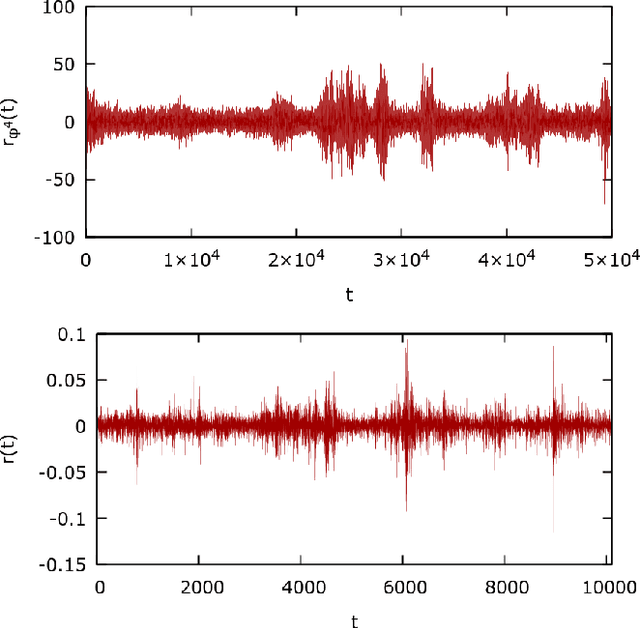
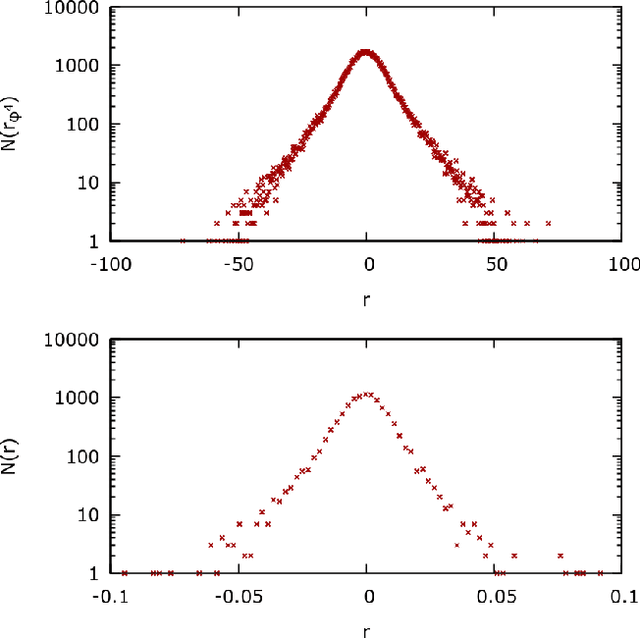
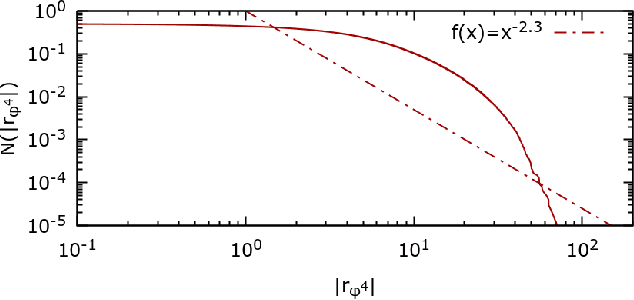
We introduce a $\phi^{4}$ lattice field theory with frustrated dynamics as a multi-agent system to reproduce stylized facts of financial markets such as fat-tailed distributions of returns and clustered volatility. Each lattice site, represented by a continuous degree of freedom, corresponds to an agent experiencing a set of competing interactions which influence its decision to buy or sell a given stock. These interactions comprise a cooperative term, which signifies that the agent should imitate the behavior of its neighbors, and a fictitious field, which compels the agent instead to conform with the opinion of the majority or the minority. To introduce the competing dynamics we exploit the Markov field structure to pursue a constructive decomposition of the $\phi^{4}$ probability distribution which we recompose with a Ferrenberg-Swendsen acceptance or rejection sampling step. We then verify numerically that the multi-agent $\phi^{4}$ field theory produces behavior observed on empirical data from the FTSE 100 London Stock Exchange index. We conclude by discussing how the presence of continuous degrees of freedom within the $\phi^{4}$ lattice field theory enables a representational capacity beyond that possible with multi-agent systems derived from Ising models.