Machine Learning Neutrino-Nucleus Cross Sections

Neutrino-nucleus scattering cross sections are critical theoretical inputs for long-baseline neutrino oscillation experiments. However, robust modeling of these cross sections remains challenging. For a simple but physically motivated toy model of the DUNE experiment, we demonstrate that an accurate neural-network model of the cross section -- leveraging Standard Model symmetries -- can be learned from near-detector data. We then perform a neutrino oscillation analysis with simulated far-detector events, finding that the modeled cross section achieves results consistent with what could be obtained if the true cross section were known exactly. This proof-of-principle study highlights the potential of future neutrino near-detector datasets and data-driven cross-section models.

Beyond 4D Tracking: Using Cluster Shapes for Track Seeding

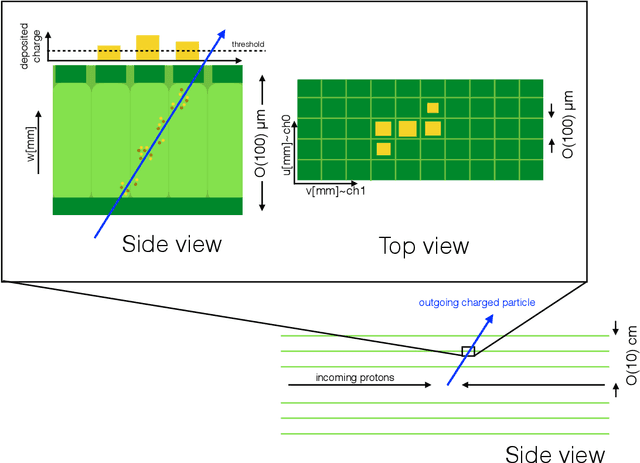
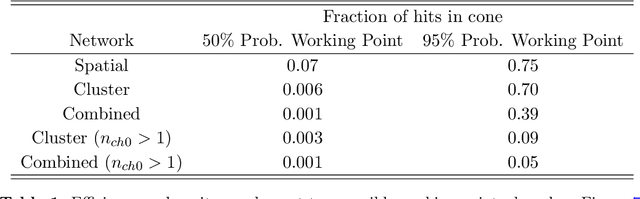
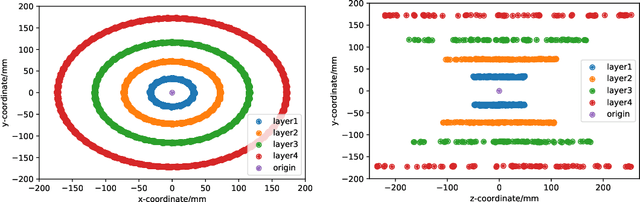
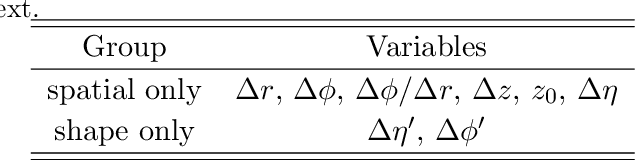
Tracking is one of the most time consuming aspects of event reconstruction at the Large Hadron Collider (LHC) and its high-luminosity upgrade (HL-LHC). Innovative detector technologies extend tracking to four-dimensions by including timing in the pattern recognition and parameter estimation. However, present and future hardware already have additional information that is largely unused by existing track seeding algorithms. The shape of clusters provides an additional dimension for track seeding that can significantly reduce the combinatorial challenge of track finding. We use neural networks to show that cluster shapes can reduce significantly the rate of fake combinatorical backgrounds while preserving a high efficiency. We demonstrate this using the information in cluster singlets, doublets and triplets. Numerical results are presented with simulations from the TrackML challenge.

i-flow: High-dimensional Integration and Sampling with Normalizing Flows

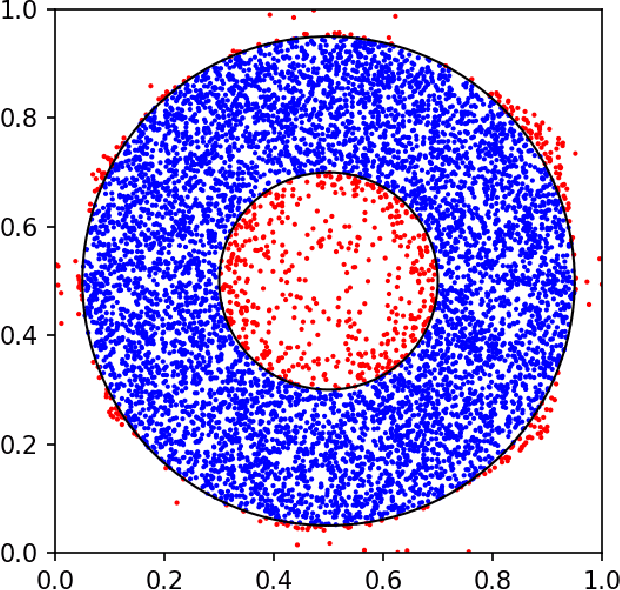
In many fields of science, high-dimensional integration is required. Numerical methods have been developed to evaluate these complex integrals. We introduce the code i-flow, a python package that performs high-dimensional numerical integration utilizing normalizing flows. Normalizing flows are machine-learned, bijective mappings between two distributions. i-flow can also be used to sample random points according to complicated distributions in high dimensions. We compare i-flow to other algorithms for high-dimensional numerical integration and show that i-flow outperforms them for high dimensional correlated integrals.