Lattice real-time simulations with learned optimal kernels

We present a simulation strategy for the real-time dynamics of quantum fields, inspired by reinforcement learning. It builds on the complex Langevin approach, which it amends with system specific prior information, a necessary prerequisite to overcome this exceptionally severe sign problem. The optimization process underlying our machine learning approach is made possible by deploying inherently stable solvers of the complex Langevin stochastic process and a novel optimality criterion derived from insight into so-called boundary terms. This conceptual and technical progress allows us to both significantly extend the range of real-time simulations in 1+1d scalar field theory beyond the state-of-the-art and to avoid discretization artifacts that plagued previous real-time field theory simulations. Limitations of and promising future directions are discussed.

Spectral Reconstruction with Deep Neural Networks

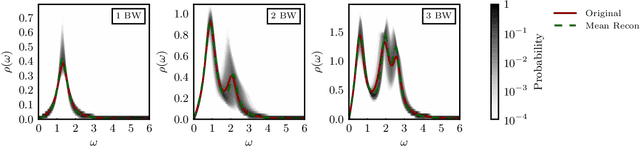
We explore artificial neural networks as a tool for the reconstruction of spectral functions from imaginary time Green's functions, a classic ill-conditioned inverse problem. Our ansatz is based on a supervised learning framework in which prior knowledge is encoded in the training data and the inverse transformation manifold is explicitly parametrised through a neural network. We systematically investigate this novel reconstruction approach, providing a detailed analysis of its performance on physically motivated mock data, and compare it to established methods of Bayesian inference. The reconstruction accuracy is found to be at least comparable, and potentially superior in particular at larger noise levels. We argue that the use of labelled training data in a supervised setting and the freedom in defining an optimisation objective are inherent advantages of the present approach and may lead to significant improvements over state-of-the-art methods in the future. Potential directions for further research are discussed in detail.