SymbolicGPT: A Generative Transformer Model for Symbolic Regression

Symbolic regression is the task of identifying a mathematical expression that best fits a provided dataset of input and output values. Due to the richness of the space of mathematical expressions, symbolic regression is generally a challenging problem. While conventional approaches based on genetic evolution algorithms have been used for decades, deep learning-based methods are relatively new and an active research area. In this work, we present SymbolicGPT, a novel transformer-based language model for symbolic regression. This model exploits the advantages of probabilistic language models like GPT, including strength in performance and flexibility. Through comprehensive experiments, we show that our model performs strongly compared to competing models with respect to the accuracy, running time, and data efficiency.

Symbolically Solving Partial Differential Equations using Deep Learning

We describe a neural-based method for generating exact or approximate solutions to differential equations in the form of mathematical expressions. Unlike other neural methods, our system returns symbolic expressions that can be interpreted directly. Our method uses a neural architecture for learning mathematical expressions to optimize a customizable objective, and is scalable, compact, and easily adaptable for a variety of tasks and configurations. The system has been shown to effectively find exact or approximate symbolic solutions to various differential equations with applications in natural sciences. In this work, we highlight how our method applies to partial differential equations over multiple variables and more complex boundary and initial value conditions.

A Neuro-Symbolic Method for Solving Differential and Functional Equations

When neural networks are used to solve differential equations, they usually produce solutions in the form of black-box functions that are not directly mathematically interpretable. We introduce a method for generating symbolic expressions to solve differential equations while leveraging deep learning training methods. Unlike existing methods, our system does not require learning a language model over symbolic mathematics, making it scalable, compact, and easily adaptable for a variety of tasks and configurations. As part of the method, we propose a novel neural architecture for learning mathematical expressions to optimize a customizable objective. The system is designed to always return a valid symbolic formula, generating a useful approximation when an exact analytic solution to a differential equation is not or cannot be found. We demonstrate through examples how our method can be applied on a number of differential equations, often obtaining symbolic approximations that are useful or insightful. Furthermore, we show how the system can be effortlessly generalized to find symbolic solutions to other mathematical tasks, including integration and functional equations.

Logic Guided Genetic Algorithms

We present a novel Auxiliary Truth enhanced Genetic Algorithm (GA) that uses logical or mathematical constraints as a means of data augmentation as well as to compute loss (in conjunction with the traditional MSE), with the aim of increasing both data efficiency and accuracy of symbolic regression (SR) algorithms. Our method, logic-guided genetic algorithm (LGGA), takes as input a set of labelled data points and auxiliary truths (ATs) (mathematical facts known a priori about the unknown function the regressor aims to learn) and outputs a specially generated and curated dataset that can be used with any SR method. Three key insights underpin our method: first, SR users often know simple ATs about the function they are trying to learn. Second, whenever an SR system produces a candidate equation inconsistent with these ATs, we can compute a counterexample to prove the inconsistency, and further, this counterexample may be used to augment the dataset and fed back to the SR system in a corrective feedback loop. Third, the value addition of these ATs is that their use in both the loss function and the data augmentation process leads to better rates of convergence, accuracy, and data efficiency. We evaluate LGGA against state-of-the-art SR tools, namely, Eureqa and TuringBot on 16 physics equations from "The Feynman Lectures on Physics" book. We find that using these SR tools in conjunction with LGGA results in them solving up to 30.0% more equations, needing only a fraction of the amount of data compared to the same tool without LGGA, i.e., resulting in up to a 61.9% improvement in data efficiency.

LGML: Logic Guided Machine Learning

We introduce Logic Guided Machine Learning (LGML), a novel approach that symbiotically combines machine learning (ML) and logic solvers with the goal of learning mathematical functions from data. LGML consists of two phases, namely a learning-phase and a logic-phase with a corrective feedback loop, such that, the learning-phase learns symbolic expressions from input data, and the logic-phase cross verifies the consistency of the learned expression with known auxiliary truths. If inconsistent, the logic-phase feeds back "counterexamples" to the learning-phase. This process is repeated until the learned expression is consistent with auxiliary truth. Using LGML, we were able to learn expressions that correspond to the Pythagorean theorem and the sine function, with several orders of magnitude improvements in data efficiency compared to an approach based on an out-of-the-box multi-layered perceptron (MLP).

Discovering Symmetry Invariants and Conserved Quantities by Interpreting Siamese Neural Networks

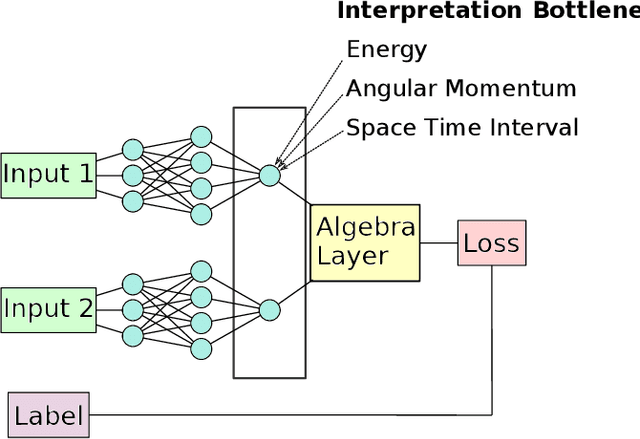
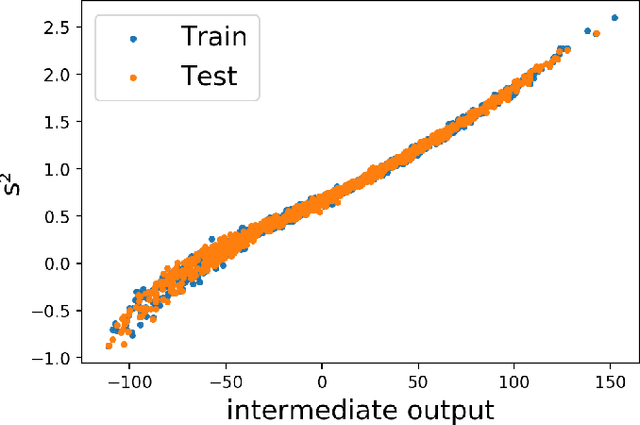
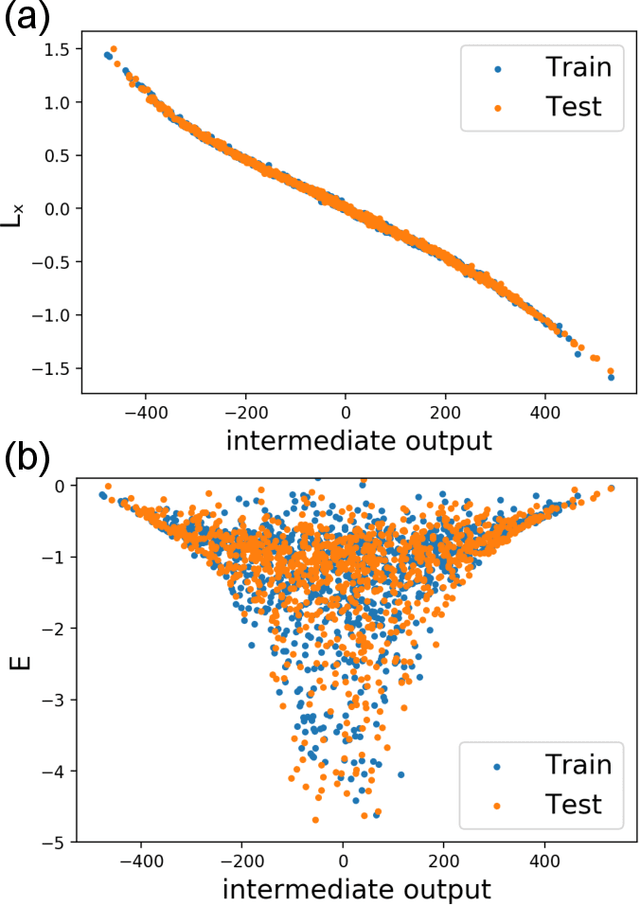
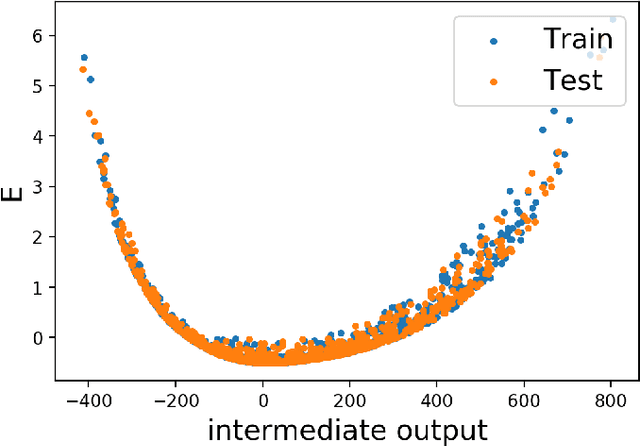
In this paper, we introduce interpretable Siamese Neural Networks (SNN) for similarity detection to the field of theoretical physics. More precisely, we apply SNNs to events in special relativity, the transformation of electromagnetic fields, and the motion of particles in a central potential. In these examples, the SNNs learn to identify datapoints belonging to the same events, field configurations, or trajectory of motion. It turns out that in the process of learning which datapoints belong to the same event or field configuration, these SNNs also learn the relevant symmetry invariants and conserved quantities. These SNNs are highly interpretable, which enables us to reveal the symmetry invariants and conserved quantities without prior knowledge.

Classification-based RNN machine translation using GRUs

We report the results of our classification-based machine translation model, built upon the framework of a recurrent neural network using gated recurrent units. Unlike other RNN models that attempt to maximize the overall conditional log probability of sentences against sentences, our model focuses a classification approach of estimating the conditional probability of the next word given the input sequence. This simpler approach using GRUs was hoped to be comparable with more complicated RNN models, but achievements in this implementation were modest and there remains a lot of room for improving this classification approach.