Yi Hong Teoh
Autoregressive model path dependence near Ising criticality
Aug 28, 2024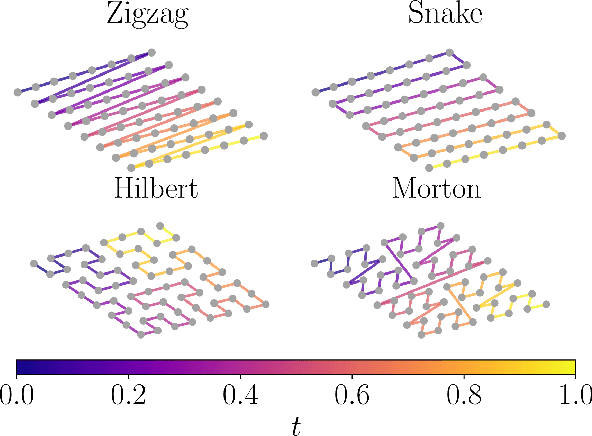
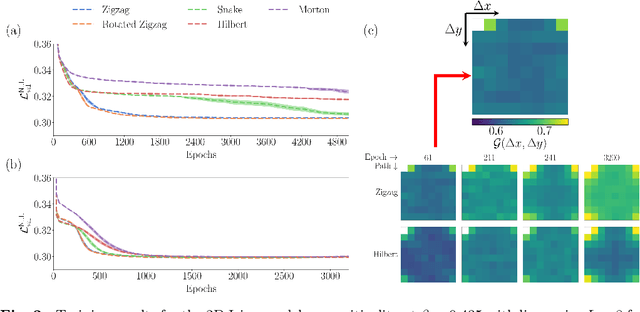
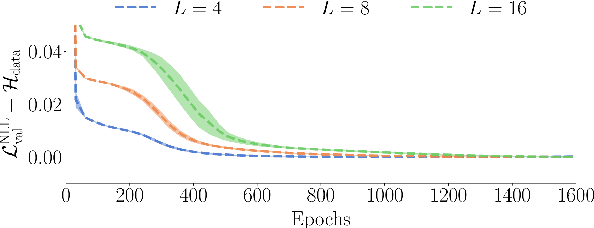
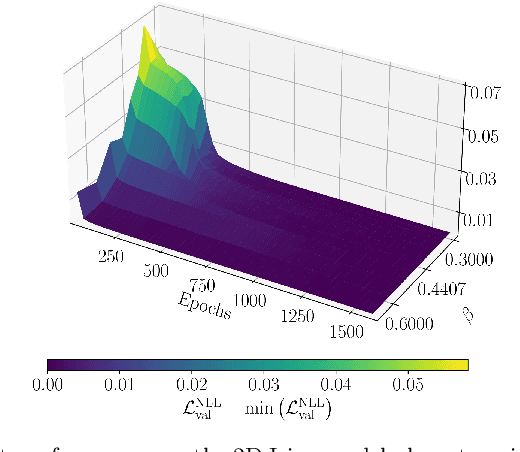
Abstract:Autoregressive models are a class of generative model that probabilistically predict the next output of a sequence based on previous inputs. The autoregressive sequence is by definition one-dimensional (1D), which is natural for language tasks and hence an important component of modern architectures like recurrent neural networks (RNNs) and transformers. However, when language models are used to predict outputs on physical systems that are not intrinsically 1D, the question arises of which choice of autoregressive sequence -- if any -- is optimal. In this paper, we study the reconstruction of critical correlations in the two-dimensional (2D) Ising model, using RNNs and transformers trained on binary spin data obtained near the thermal phase transition. We compare the training performance for a number of different 1D autoregressive sequences imposed on finite-size 2D lattices. We find that paths with long 1D segments are more efficient at training the autoregressive models compared to space-filling curves that better preserve the 2D locality. Our results illustrate the potential importance in choosing the optimal autoregressive sequence ordering when training modern language models for tasks in physics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge