Neural Network Field Theories: Non-Gaussianity, Actions, and Locality

Both the path integral measure in field theory and ensembles of neural networks describe distributions over functions. When the central limit theorem can be applied in the infinite-width (infinite-$N$) limit, the ensemble of networks corresponds to a free field theory. Although an expansion in $1/N$ corresponds to interactions in the field theory, others, such as in a small breaking of the statistical independence of network parameters, can also lead to interacting theories. These other expansions can be advantageous over the $1/N$-expansion, for example by improved behavior with respect to the universal approximation theorem. Given the connected correlators of a field theory, one can systematically reconstruct the action order-by-order in the expansion parameter, using a new Feynman diagram prescription whose vertices are the connected correlators. This method is motivated by the Edgeworth expansion and allows one to derive actions for neural network field theories. Conversely, the correspondence allows one to engineer architectures realizing a given field theory by representing action deformations as deformations of neural network parameter densities. As an example, $\phi^4$ theory is realized as an infinite-$N$ neural network field theory.

Symmetry-via-Duality: Invariant Neural Network Densities from Parameter-Space Correlators

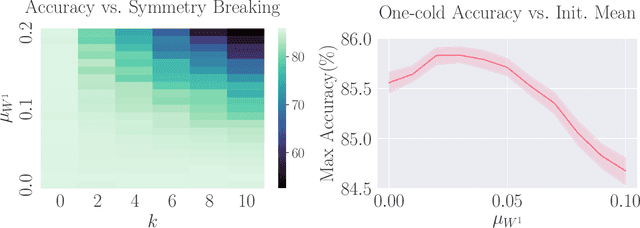
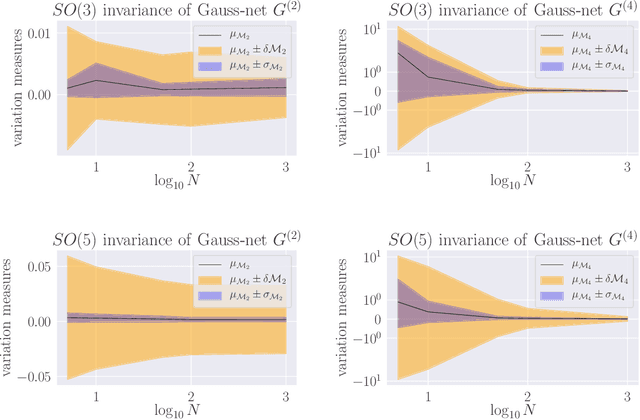
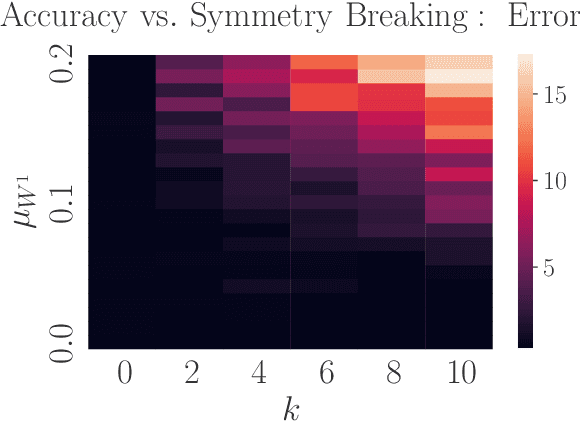
Parameter-space and function-space provide two different duality frames in which to study neural networks. We demonstrate that symmetries of network densities may be determined via dual computations of network correlation functions, even when the density is unknown and the network is not equivariant. Symmetry-via-duality relies on invariance properties of the correlation functions, which stem from the choice of network parameter distributions. Input and output symmetries of neural network densities are determined, which recover known Gaussian process results in the infinite width limit. The mechanism may also be utilized to determine symmetries during training, when parameters are correlated, as well as symmetries of the Neural Tangent Kernel. We demonstrate that the amount of symmetry in the initialization density affects the accuracy of networks trained on Fashion-MNIST, and that symmetry breaking helps only when it is in the direction of ground truth.

Neural Networks and Quantum Field Theory

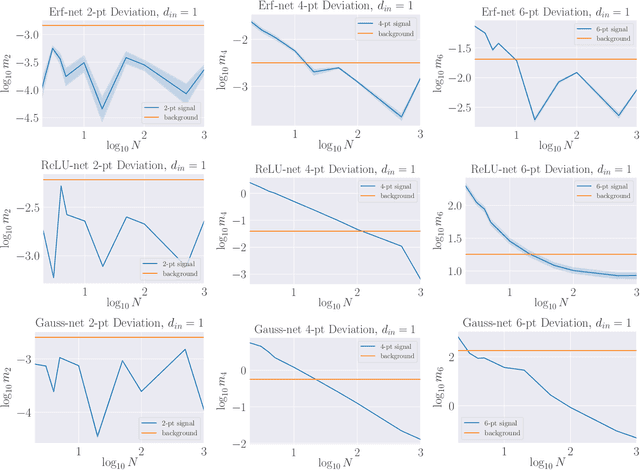
We propose a theoretical understanding of neural networks in terms of Wilsonian effective field theory. The correspondence relies on the fact that many asymptotic neural networks are drawn from Gaussian processes, the analog of non-interacting field theories. Moving away from the asymptotic limit yields a non-Gaussian process and corresponds to turning on particle interactions, allowing for the computation of correlation functions of neural network outputs with Feynman diagrams. Minimal non-Gaussian process likelihoods are determined by the most relevant non-Gaussian terms, according to the flow in their coefficients induced by the Wilsonian renormalization group. This yields a direct connection between overparameterization and simplicity of neural network likelihoods. Whether the coefficients are constants or functions may be understood in terms of GP limit symmetries, as expected from 't Hooft's technical naturalness. General theoretical calculations are matched to neural network experiments in the simplest class of models allowing the correspondence. Our formalism is valid for any of the many architectures that becomes a GP in an asymptotic limit, a property preserved under certain types of training.