Learning the Simplicity of Scattering Amplitudes

The simplification and reorganization of complex expressions lies at the core of scientific progress, particularly in theoretical high-energy physics. This work explores the application of machine learning to a particular facet of this challenge: the task of simplifying scattering amplitudes expressed in terms of spinor-helicity variables. We demonstrate that an encoder-decoder transformer architecture achieves impressive simplification capabilities for expressions composed of handfuls of terms. Lengthier expressions are implemented in an additional embedding network, trained using contrastive learning, which isolates subexpressions that are more likely to simplify. The resulting framework is capable of reducing expressions with hundreds of terms - a regular occurrence in quantum field theory calculations - to vastly simpler equivalent expressions. Starting from lengthy input expressions, our networks can generate the Parke-Taylor formula for five-point gluon scattering, as well as new compact expressions for five-point amplitudes involving scalars and gravitons. An interactive demonstration can be found at https://spinorhelicity.streamlit.app .

Reconstructing $S$-matrix Phases with Machine Learning

An important element of the $S$-matrix bootstrap program is the relationship between the modulus of an $S$-matrix element and its phase. Unitarity relates them by an integral equation. Even in the simplest case of elastic scattering, this integral equation cannot be solved analytically and numerical approaches are required. We apply modern machine learning techniques to studying the unitarity constraint. We find that for a given modulus, when a phase exists it can generally be reconstructed to good accuracy with machine learning. Moreover, the loss of the reconstruction algorithm provides a good proxy for whether a given modulus can be consistent with unitarity at all. In addition, we study the question of whether multiple phases can be consistent with a single modulus, finding novel phase-ambiguous solutions. In particular, we find a new phase-ambiguous solution which pushes the known limit on such solutions significantly beyond the previous bound.

Neural Network Field Theories: Non-Gaussianity, Actions, and Locality

Both the path integral measure in field theory and ensembles of neural networks describe distributions over functions. When the central limit theorem can be applied in the infinite-width (infinite-$N$) limit, the ensemble of networks corresponds to a free field theory. Although an expansion in $1/N$ corresponds to interactions in the field theory, others, such as in a small breaking of the statistical independence of network parameters, can also lead to interacting theories. These other expansions can be advantageous over the $1/N$-expansion, for example by improved behavior with respect to the universal approximation theorem. Given the connected correlators of a field theory, one can systematically reconstruct the action order-by-order in the expansion parameter, using a new Feynman diagram prescription whose vertices are the connected correlators. This method is motivated by the Edgeworth expansion and allows one to derive actions for neural network field theories. Conversely, the correspondence allows one to engineer architectures realizing a given field theory by representing action deformations as deformations of neural network parameter densities. As an example, $\phi^4$ theory is realized as an infinite-$N$ neural network field theory.

Simplifying Polylogarithms with Machine Learning

Polylogrithmic functions, such as the logarithm or dilogarithm, satisfy a number of algebraic identities. For the logarithm, all the identities follow from the product rule. For the dilogarithm and higher-weight classical polylogarithms, the identities can involve five functions or more. In many calculations relevant to particle physics, complicated combinations of polylogarithms often arise from Feynman integrals. Although the initial expressions resulting from the integration usually simplify, it is often difficult to know which identities to apply and in what order. To address this bottleneck, we explore to what extent machine learning methods can help. We consider both a reinforcement learning approach, where the identities are analogous to moves in a game, and a transformer network approach, where the problem is viewed analogously to a language-translation task. While both methods are effective, the transformer network appears more powerful and holds promise for practical use in symbolic manipulation tasks in mathematical physics.

Challenges for Unsupervised Anomaly Detection in Particle Physics

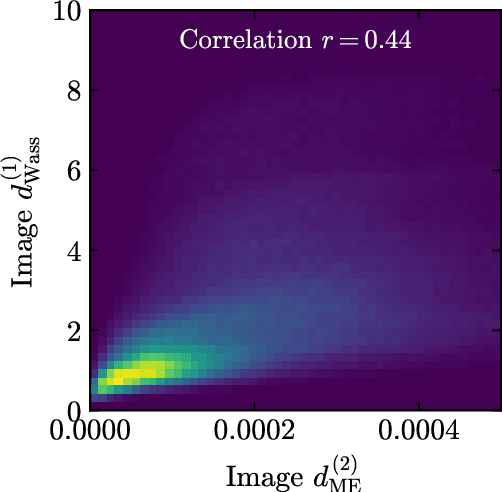
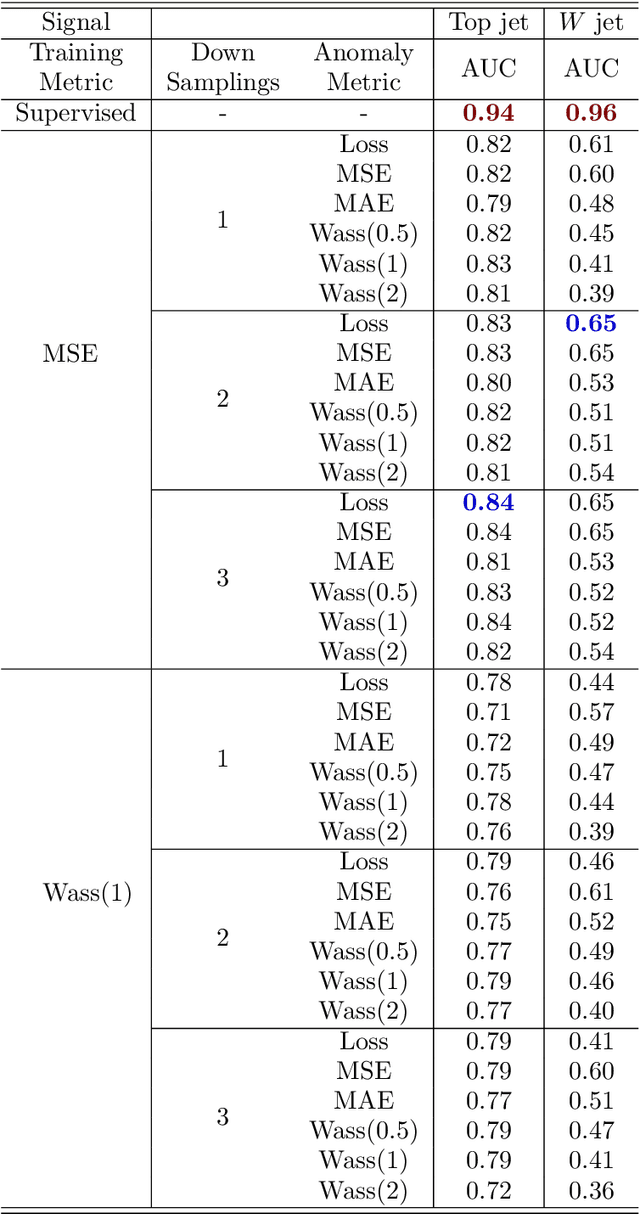
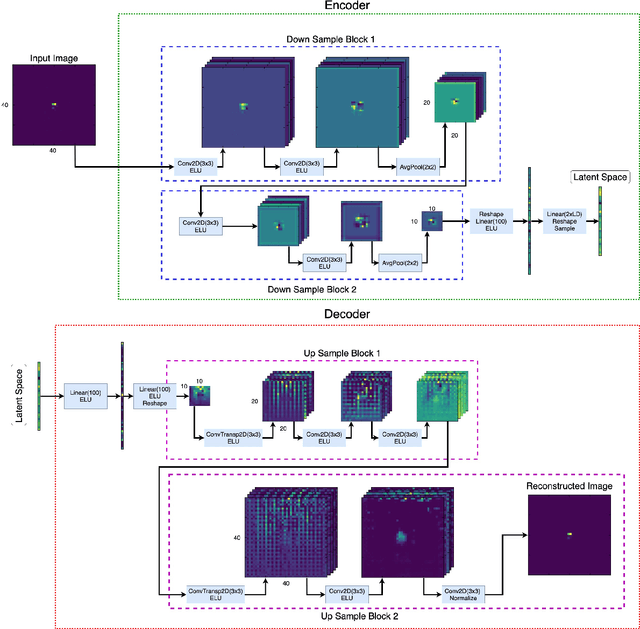
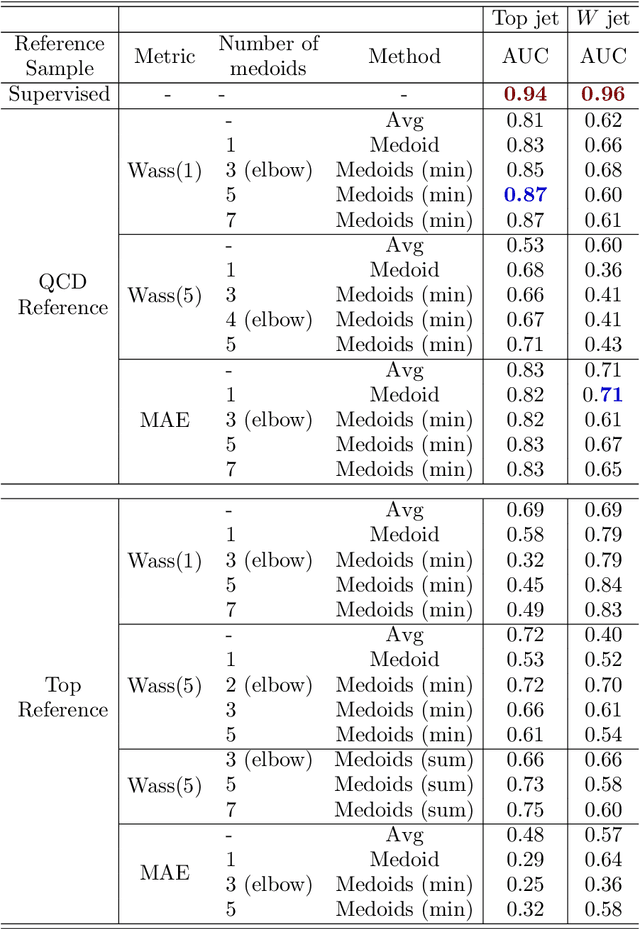
Anomaly detection relies on designing a score to determine whether a particular event is uncharacteristic of a given background distribution. One way to define a score is to use autoencoders, which rely on the ability to reconstruct certain types of data (background) but not others (signals). In this paper, we study some challenges associated with variational autoencoders, such as the dependence on hyperparameters and the metric used, in the context of anomalous signal (top and $W$) jets in a QCD background. We find that the hyperparameter choices strongly affect the network performance and that the optimal parameters for one signal are non-optimal for another. In exploring the networks, we uncover a connection between the latent space of a variational autoencoder trained using mean-squared-error and the optimal transport distances within the dataset. We then show that optimal transport distances to representative events in the background dataset can be used directly for anomaly detection, with performance comparable to the autoencoders. Whether using autoencoders or optimal transport distances for anomaly detection, we find that the choices that best represent the background are not necessarily best for signal identification. These challenges with unsupervised anomaly detection bolster the case for additional exploration of semi-supervised or alternative approaches.

Jet Charge and Machine Learning

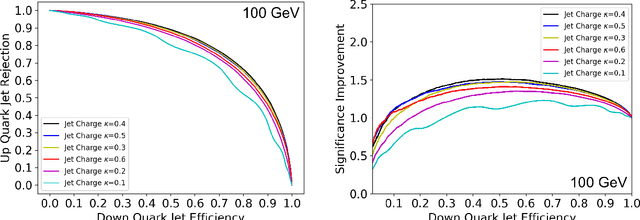
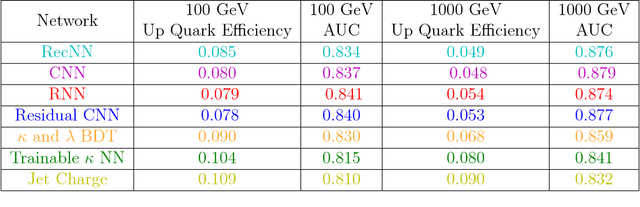
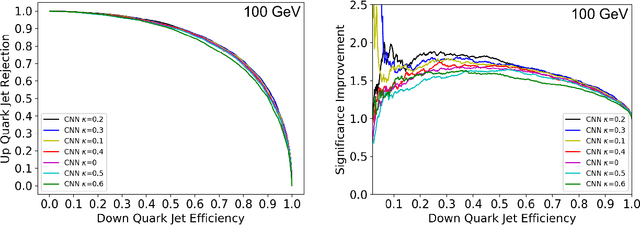
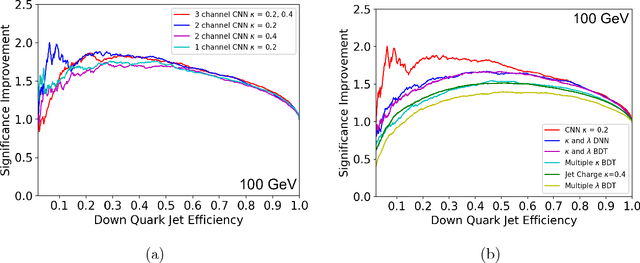
Modern machine learning techniques, such as convolutional, recurrent and recursive neural networks, have shown promise for jet substructure at the Large Hadron Collider. For example, they have demonstrated effectiveness at boosted top or W boson identification or for quark/gluon discrimination. We explore these methods for the purpose of classifying jets according to their electric charge. We find that both neural networks that incorporate distance within the jet as an input and boosted decision trees including radial distance information can provide significant improvement in jet charge extraction over current methods. Specifically, convolutional, recurrent, and recursive networks can provide the largest improvement over traditional methods, in part by effectively utilizing distance within the jet or clustering history. The advantages of using a fixed-size input representation (as with the CNN) or a small input representation (as with the RNN) suggest that both convolutional and recurrent networks will be essential to the future of modern machine learning at colliders.

Deep learning in color: towards automated quark/gluon jet discrimination

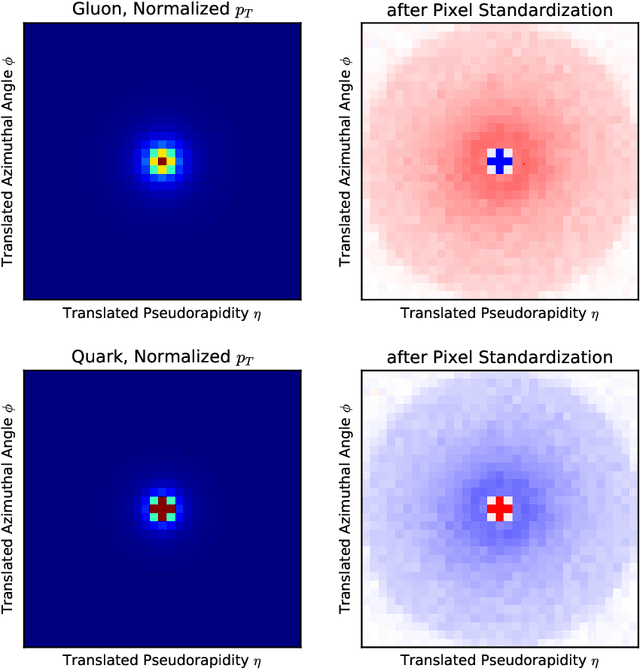
Artificial intelligence offers the potential to automate challenging data-processing tasks in collider physics. To establish its prospects, we explore to what extent deep learning with convolutional neural networks can discriminate quark and gluon jets better than observables designed by physicists. Our approach builds upon the paradigm that a jet can be treated as an image, with intensity given by the local calorimeter deposits. We supplement this construction by adding color to the images, with red, green and blue intensities given by the transverse momentum in charged particles, transverse momentum in neutral particles, and pixel-level charged particle counts. Overall, the deep networks match or outperform traditional jet variables. We also find that, while various simulations produce different quark and gluon jets, the neural networks are surprisingly insensitive to these differences, similar to traditional observables. This suggests that the networks can extract robust physical information from imperfect simulations.

Learning to Classify from Impure Samples with High-Dimensional Data

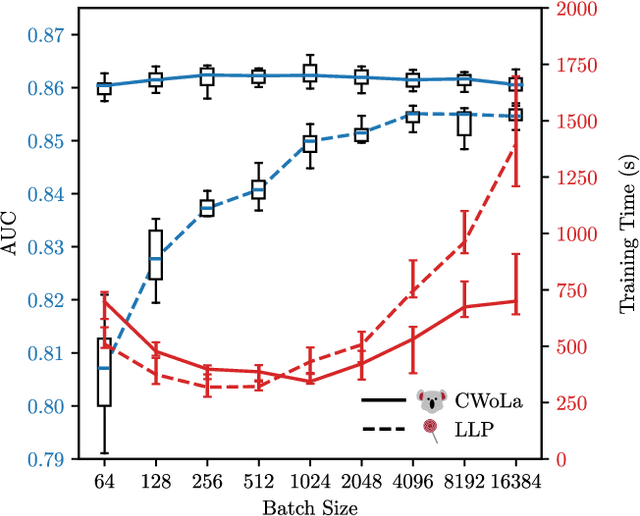
A persistent challenge in practical classification tasks is that labeled training sets are not always available. In particle physics, this challenge is surmounted by the use of simulations. These simulations accurately reproduce most features of data, but cannot be trusted to capture all of the complex correlations exploitable by modern machine learning methods. Recent work in weakly supervised learning has shown that simple, low-dimensional classifiers can be trained using only the impure mixtures present in data. Here, we demonstrate that complex, high-dimensional classifiers can also be trained on impure mixtures using weak supervision techniques, with performance comparable to what could be achieved with pure samples. Using weak supervision will therefore allow us to avoid relying exclusively on simulations for high-dimensional classification. This work opens the door to a new regime whereby complex models are trained directly on data, providing direct access to probe the underlying physics.

JUNIPR: a Framework for Unsupervised Machine Learning in Particle Physics

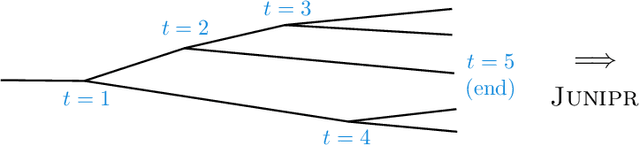
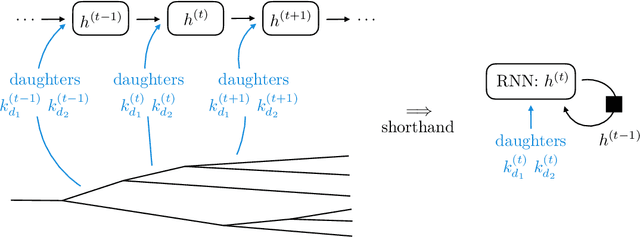
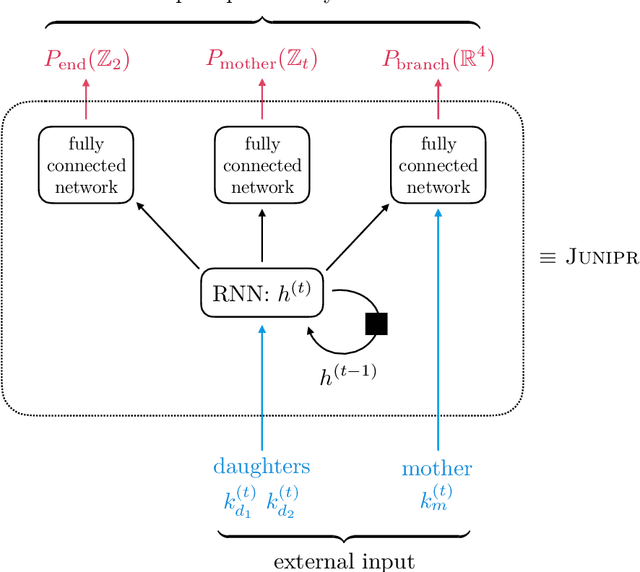
In applications of machine learning to particle physics, a persistent challenge is how to go beyond discrimination to learn about the underlying physics. To this end, a powerful tool would be a framework for unsupervised learning, where the machine learns the intricate high-dimensional contours of the data upon which it is trained, without reference to pre-established labels. In order to approach such a complex task, an unsupervised network must be structured intelligently, based on a qualitative understanding of the data. In this paper, we scaffold the neural network's architecture around a leading-order model of the physics underlying the data. In addition to making unsupervised learning tractable, this design actually alleviates existing tensions between performance and interpretability. We call the framework JUNIPR: "Jets from UNsupervised Interpretable PRobabilistic models". In this approach, the set of particle momenta composing a jet are clustered into a binary tree that the neural network examines sequentially. Training is unsupervised and unrestricted: the network could decide that the data bears little correspondence to the chosen tree structure. However, when there is a correspondence, the network's output along the tree has a direct physical interpretation. JUNIPR models can perform discrimination tasks, through the statistically optimal likelihood-ratio test, and they permit visualizations of discrimination power at each branching in a jet's tree. Additionally, JUNIPR models provide a probability distribution from which events can be drawn, providing a data-driven Monte Carlo generator. As a third application, JUNIPR models can reweight events from one (e.g. simulated) data set to agree with distributions from another (e.g. experimental) data set.

Pileup Mitigation with Machine Learning (PUMML)

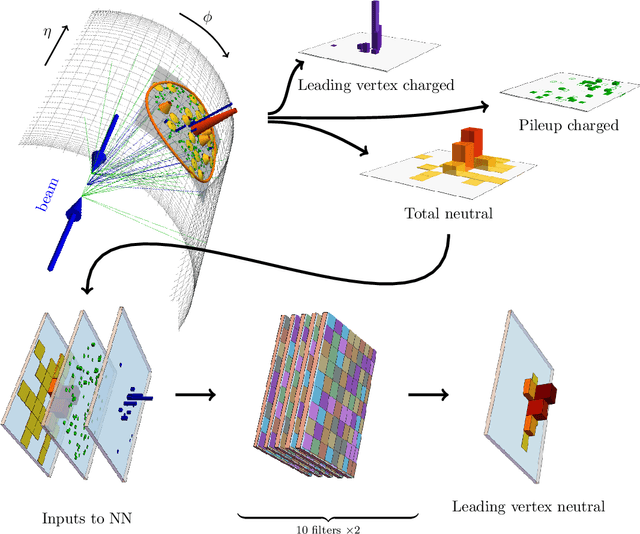
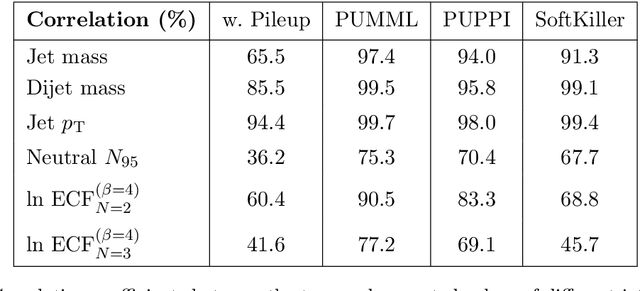
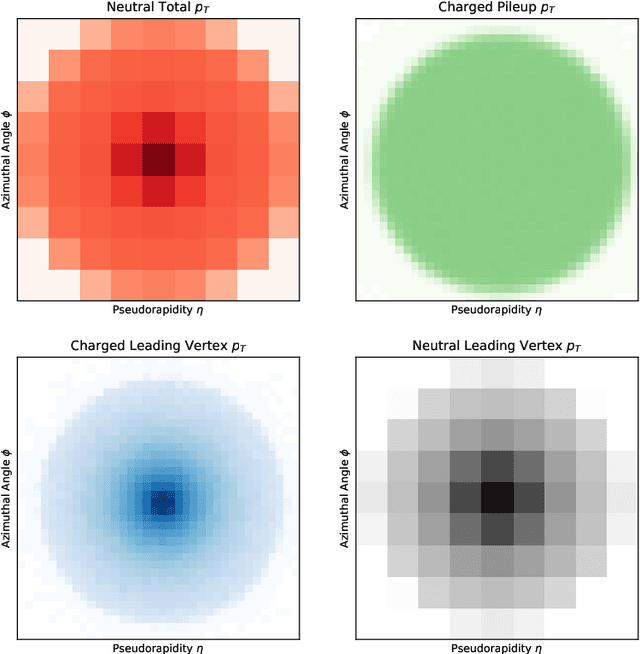
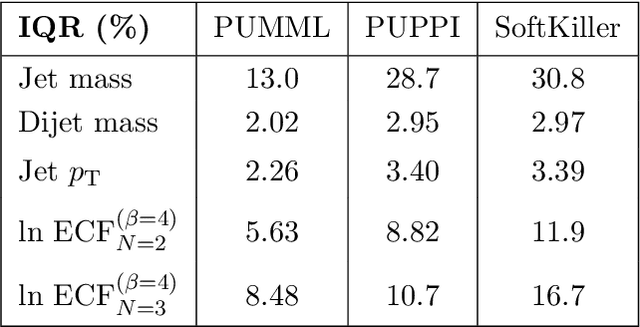
Pileup involves the contamination of the energy distribution arising from the primary collision of interest (leading vertex) by radiation from soft collisions (pileup). We develop a new technique for removing this contamination using machine learning and convolutional neural networks. The network takes as input the energy distribution of charged leading vertex particles, charged pileup particles, and all neutral particles and outputs the energy distribution of particles coming from leading vertex alone. The PUMML algorithm performs remarkably well at eliminating pileup distortion on a wide range of simple and complex jet observables. We test the robustness of the algorithm in a number of ways and discuss how the network can be trained directly on data.