Networks of Networks: Complexity Class Principles Applied to Compound AI Systems Design
Paper and Code
Jul 23, 2024
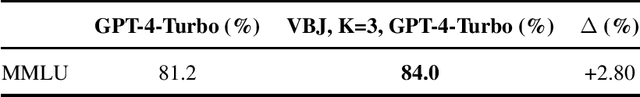
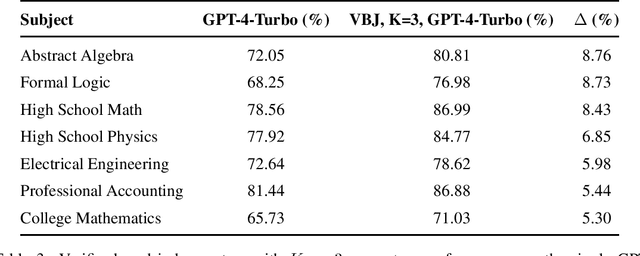

As practitioners seek to surpass the current reliability and quality frontier of monolithic models, Compound AI Systems consisting of many language model inference calls are increasingly employed. In this work, we construct systems, which we call Networks of Networks (NoNs) organized around the distinction between generating a proposed answer and verifying its correctness, a fundamental concept in complexity theory that we show empirically extends to Language Models (LMs). We introduce a verifier-based judge NoN with K generators, an instantiation of "best-of-K" or "judge-based" compound AI systems. Through experiments on synthetic tasks such as prime factorization, and core benchmarks such as the MMLU, we demonstrate notable performance gains. For instance, in factoring products of two 3-digit primes, a simple NoN improves accuracy from 3.7\% to 36.6\%. On MMLU, a verifier-based judge construction with only 3 generators boosts accuracy over individual GPT-4-Turbo calls by 2.8\%. Our analysis reveals that these gains are most pronounced in domains where verification is notably easier than generation--a characterization which we believe subsumes many reasoning and procedural knowledge tasks, but doesn't often hold for factual and declarative knowledge-based settings. For mathematical and formal logic reasoning-based subjects of MMLU, we observe a 5-8\% or higher gain, whilst no gain on others such as geography and religion. We provide key takeaways for ML practitioners, including the importance of considering verification complexity, the impact of witness format on verifiability, and a simple test to determine the potential benefit of this NoN approach for a given problem distribution. This work aims to inform future research and practice in the design of compound AI systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge