Dense Associative Memory Through the Lens of Random Features
Paper and Code
Oct 31, 2024

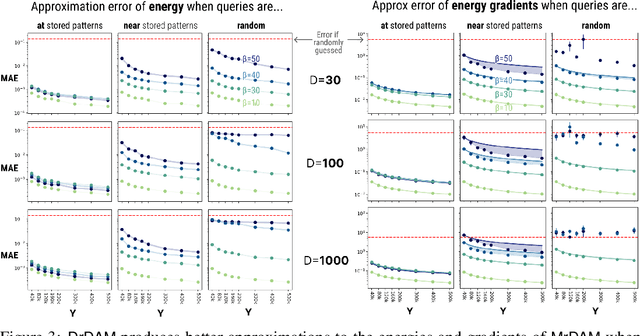
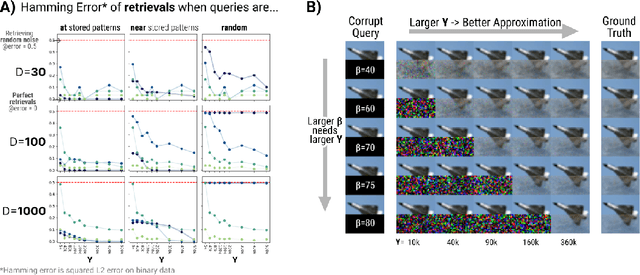
Dense Associative Memories are high storage capacity variants of the Hopfield networks that are capable of storing a large number of memory patterns in the weights of the network of a given size. Their common formulations typically require storing each pattern in a separate set of synaptic weights, which leads to the increase of the number of synaptic weights when new patterns are introduced. In this work we propose an alternative formulation of this class of models using random features, commonly used in kernel methods. In this formulation the number of network's parameters remains fixed. At the same time, new memories can be added to the network by modifying existing weights. We show that this novel network closely approximates the energy function and dynamics of conventional Dense Associative Memories and shares their desirable computational properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge