Reinforcement Learning of Adaptive Acquisition Policies for Inverse Problems
Paper and Code
Jul 10, 2024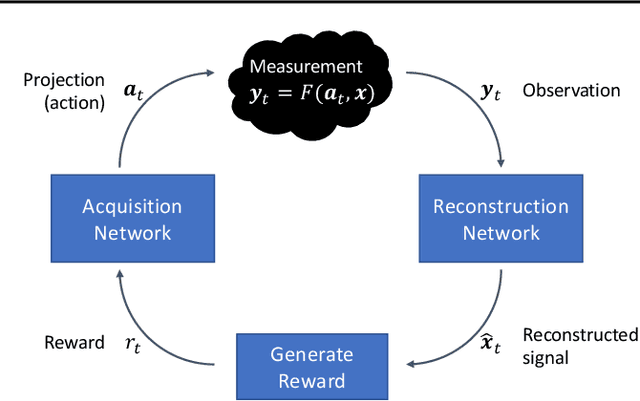

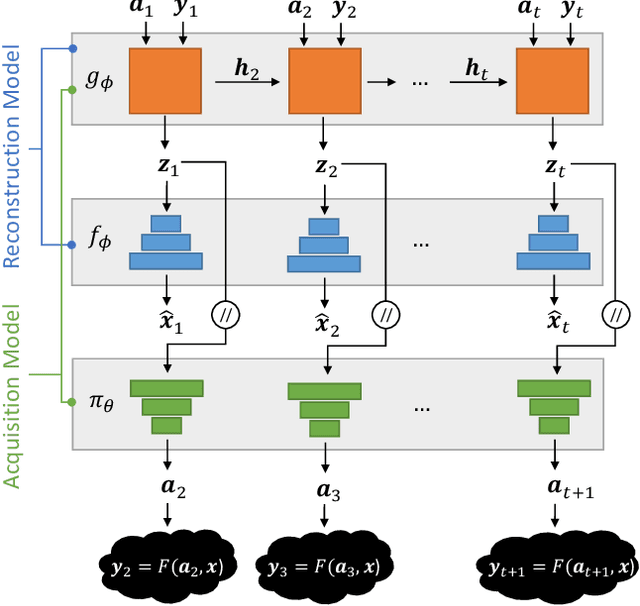

A promising way to mitigate the expensive process of obtaining a high-dimensional signal is to acquire a limited number of low-dimensional measurements and solve an under-determined inverse problem by utilizing the structural prior about the signal. In this paper, we focus on adaptive acquisition schemes to save further the number of measurements. To this end, we propose a reinforcement learning-based approach that sequentially collects measurements to better recover the underlying signal by acquiring fewer measurements. Our approach applies to general inverse problems with continuous action spaces and jointly learns the recovery algorithm. Using insights obtained from theoretical analysis, we also provide a probabilistic design for our methods using variational formulation. We evaluate our approach on multiple datasets and with two measurement spaces (Gaussian, Radon). Our results confirm the benefits of adaptive strategies in low-acquisition horizon settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge